離散数学 (全64問中14問目)
No.14
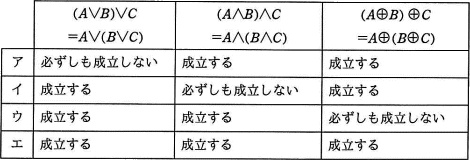
論理和(∨),論理積(∧),排他的論理和(⊕)の結合法則の成立に関する記述として,適切な組合せはどれか。
出典:平成29年春期 問1
- [出題歴]
- 応用情報技術者 H21秋期 問2
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
エ
解説
論理演算の演算則の一つに「結合の法則」があります。
論理演算は集合演算と同様の性質を持っているので、上記の「結合の法則」をベン図を用いて表すと次のようになります。
[論理和]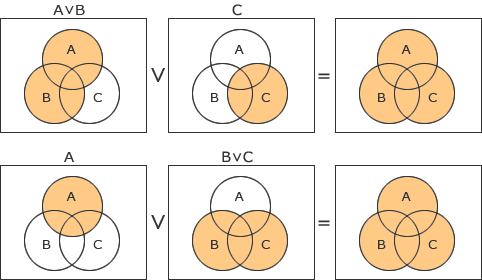 [論理積]
[論理積]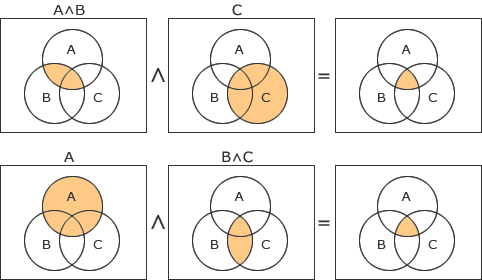 [排他的論理和]
[排他的論理和]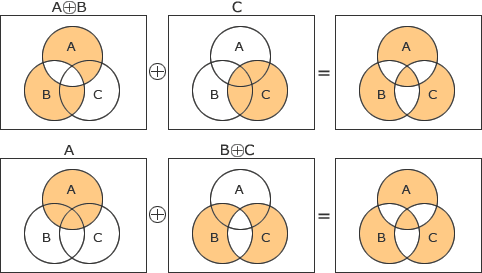 またA,B,Cそれぞれの0,1の組み合わせを入力とした真理値表を作成する方法でも正解にたどりつくことができます。
またA,B,Cそれぞれの0,1の組み合わせを入力とした真理値表を作成する方法でも正解にたどりつくことができます。
- (A・B)・C=A・(B・C)
- (A+B)+C=A+(B+C)
論理演算は集合演算と同様の性質を持っているので、上記の「結合の法則」をベン図を用いて表すと次のようになります。
[論理和]