離散数学 (全64問中17問目)
No.17
10進数123を,英字A~Zを用いた26進数で表したものはどれか。ここで,A=0,B=1,…,Z=25とする。
出典:平成28年春期 問2
- BCD
- DCB
- ET
- TE
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ウ
解説
10進数123を26で割ると、商と余りは以下のようになります。
123÷26=4余り19
つまり10進数123は、(261×4)+19と表せます。英字と数字は以下のように対応しているため、各桁を4→E,19→Tと置き換えると26進数「ET」になります。したがって「ウ」が正解です。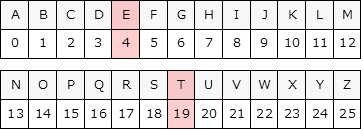
123÷26=4余り19
つまり10進数123は、(261×4)+19と表せます。英字と数字は以下のように対応しているため、各桁を4→E,19→Tと置き換えると26進数「ET」になります。したがって「ウ」が正解です。

