離散数学 (全64問中20問目)
No.20
A,B,C,Dを論理変数とするとき,次のカルノー図と等価な論理式はどれか。ここで,・は論理積,+は論理和,XはXの否定を表す。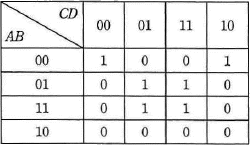

出典:平成26年秋期 問1
- A・B・C・D+B・D
- A・B・C・D+B・D
- A・B・D+B・D
- A・B・D+B・D
- [出題歴]
- 応用情報技術者 R4秋期 問2
- ソフトウェア開発技術者 H17秋期 問5
- ソフトウェア開発技術者 H19春期 問5
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
エ
解説
カルノー図は、行と列それぞれに記述された論理変数の組合せの結果が"真"となる場合に"1"を、"偽"となる場合に"0"を、その該当セルに書きこむことで論理式を図で表す方法です。
カルノー図から論理式を導くには、表の中のすべての"1"が記入されているセルをグループ化して共通項を取り出すのですが、このグループ化は以下のという3つのルールに従って行います。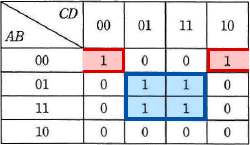 次にグループごとに共通項を取り出して、その論理積を作ります。
次にグループごとに共通項を取り出して、その論理積を作ります。
カルノー図から論理式を導くには、表の中のすべての"1"が記入されているセルをグループ化して共通項を取り出すのですが、このグループ化は以下のという3つのルールに従って行います。
- グループ化するすべてのセルの値は"1"であること
- グループ化するセルの数は2nであること
- カルノー図の上下の端および左右の端は連続していると考える

- 赤い枠で囲ったグループは、A B C DとA B C Dなので、共通項はA B D、論理積はA・B・Dになります。
- 青い枠で囲ったグループは、A B C D、A B C D、A B C D、A B C Dなので、共通項はB D、論理積はB・Dになります。
