離散数学 (全64問中35問目)
No.35
図に示す16ビットの浮動小数点形式において,10進数 0.25 を正規化した表現はどれか。ここで,正規化は仮数部の最上位けたが1になるように指数部と仮数部を調節する操作とする。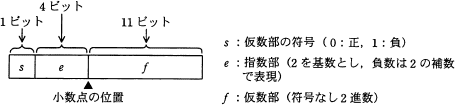

出典:平成22年春期 問2
- [出題歴]
- 基本情報技術者 H18春期 問4
- ソフトウェア開発技術者 H19秋期 問2
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ウ
解説
10進数0.25は2進数に変換すると0.01です。この2進数0.01を問題文にあるように正規化すると0.1×2-1と表現することができます。
この0.1×2-1 を浮動小数点形式の各桁に当てはめていきます。
s:10進数0.25は正の値なので、s には0が入ります。
e: 指数は -1なので、これを4ビットの2の補数であらわした1111が入ります。
f: 仮数部は、0.1なので小数点の右側部分である1がそのまま入り 10000000000 になります。
(fの部分はすべての選択肢で共通なので考える必要はありませんが…)
つまり答えは、0111110000000000で「ウ」となります。
※正規化するとき2進数0.01を、0.1×2-1に変換する箇所について補足説明のご依頼がありましたので追記します。
正規化は、仮数部の有効桁数を最大にするためにおこなう操作です。
10進数0.25は2進数に変換すると0.01です。
正規化するには、小数点第1位に1が来るようにしたいので、この問題の場合は小数点を1つ右へ移動したいわけです。
0.01(2)は2進数なので2倍してやると0.1(2)になって小数第1位が適切な形式になります。
0.01(2)×2=0.1(2)
シフト演算のように考えて、小数点を
{
n回右に移動すると2の n乗倍
n回左に移動すると2の -n乗倍
}
という関係です。
0.1(2)は、0.01(2)を2倍した数ですから、
0.01(2)は、0.1(2)の1/2倍という関係になります。
0.01(2)=0.1(2)×1/2
この1/2を2の累乗で表わすと2の-1乗ですので、
0.01(2)=0.1(2)×2-1
という表現に変換できるわけです。
この0.1×2-1 を浮動小数点形式の各桁に当てはめていきます。
s:10進数0.25は正の値なので、s には0が入ります。
e: 指数は -1なので、これを4ビットの2の補数であらわした1111が入ります。
f: 仮数部は、0.1なので小数点の右側部分である1がそのまま入り 10000000000 になります。
(fの部分はすべての選択肢で共通なので考える必要はありませんが…)
つまり答えは、0111110000000000で「ウ」となります。
※正規化するとき2進数0.01を、0.1×2-1に変換する箇所について補足説明のご依頼がありましたので追記します。
正規化は、仮数部の有効桁数を最大にするためにおこなう操作です。
10進数0.25は2進数に変換すると0.01です。
正規化するには、小数点第1位に1が来るようにしたいので、この問題の場合は小数点を1つ右へ移動したいわけです。
0.01(2)は2進数なので2倍してやると0.1(2)になって小数第1位が適切な形式になります。
0.01(2)×2=0.1(2)
シフト演算のように考えて、小数点を
{
n回右に移動すると2の n乗倍
n回左に移動すると2の -n乗倍
}
という関係です。
0.1(2)は、0.01(2)を2倍した数ですから、
0.01(2)は、0.1(2)の1/2倍という関係になります。
0.01(2)=0.1(2)×1/2
この1/2を2の累乗で表わすと2の-1乗ですので、
0.01(2)=0.1(2)×2-1
という表現に変換できるわけです。
