応用数学 (全54問中24問目)
No.24
グラフに示される頂点V1からV4,V5,V6の各点への最短所要時間を求め,短い順に並べたものはどれか。ここで,グラフ中の数値は各区間の所要時間を表すものとし,最短所要時間が同ーの場合には添字の小さい順に並べるものとする。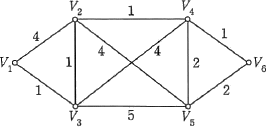

出典:平成26年秋期 問5
- V4,V5,V6
- V4,V6,V5
- V5,V4,V6
- V5,V6,V4
分類
テクノロジ系 » 基礎理論 » 応用数学
正解
イ
解説
[V4への最短経路]
V1→V3→V2→V4 で最短時間は 3 です。
[V5への最短経路]
V1→V3→V2→V4→V5 で最短時間は 5 です。
[V6への最短経路]
V1→V3→V2→V4→V6 で最短時間は 4 です。
よって短い順に並べると「V4,V6,V5」になります。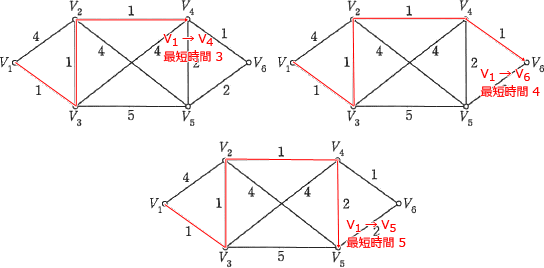
V1→V3→V2→V4 で最短時間は 3 です。
[V5への最短経路]
V1→V3→V2→V4→V5 で最短時間は 5 です。
[V6への最短経路]
V1→V3→V2→V4→V6 で最短時間は 4 です。
よって短い順に並べると「V4,V6,V5」になります。

