データ構造(全39問中22問目)
No.22解説へ
PUSH命令でスタックにデータを入れ,POP命令でスタックからデータを取り出す。動作中のプログラムにおいて,ある状態から次の順で10個の命令を実行したとき,スタックの中のデータは図のようになった。1番目のPUSH命令でスタックに入れたデータはどれか。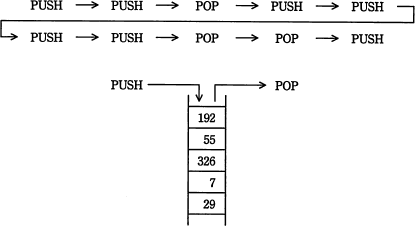

出典:平成23年特別 問 7
- 29
- 7
- 326
- 55
広告
解説
実行された10命令を一つずつ戻りながら、最初のPUSH命令までさかのぼっていきます。
実行された命令を遡りたいので、通常の操作とは逆に考えて、PUSH命令の時は、「スタックの一番上のデータを取り除く」、POP命令の時には「スタックの一番上にデータを積む」というようにしていきます。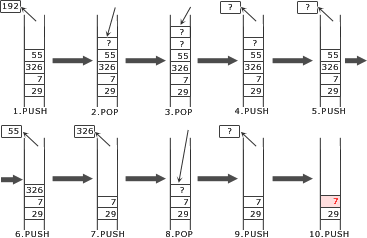
実行された命令を遡りたいので、通常の操作とは逆に考えて、PUSH命令の時は、「スタックの一番上のデータを取り除く」、POP命令の時には「スタックの一番上にデータを積む」というようにしていきます。
- PUSH スタックの一番上にあるデータは「192」なので、これを取り除きます。
- POP 取り出されたデータ「?」(値が不明)をスタックに積みます。
- POP 取り出されたデータ「?」をスタックに積みます。
- PUSH スタックの一番上にあるデータ「?」を取り除きます。
- PUSH スタックの一番上にあるデータ「?」を取り除きます。
- PUSH スタックの一番上にあるデータ「55」を取り除きます。
- PUSH スタックの一番上にあるデータ「326」を取り除きます。
- POP 取り出されたデータ「?」をスタックに積みます。
- PUSH スタックの一番上にあるデータ「?」を取り除きます。
- これが最初のPUSH命令です。スタックの一番上にあるデータは「7」なので、1番目の命令では「7」がPUSHされたことがわかります。
