解説

〔アについて〕
オーダー記法は、アルゴリズムの計算量を入力データ数Nとの関係で表す表記法です。次のような例があります。

• O(1)　入力数に関係なく計算量は一定（定数時間）
• O(N)　入力数に比例して計算量が増える（線形時間）
• O(N²)　入力数の2乗に比例して計算量が増える（二次時間）
• O(log N)　入力数に対して計算量が対数的に増加（対数時間）

プログラムの時間計算量を求めるには、繰返し処理（ループ）が何回実行されるかを調べることが重要です。

図1のプログラムを見ると二重のwhileループがあります。
外側のwhileループでは、変数dを2からNまで1ずつ増やしながら繰り返しているので、実行回数は(N－1)回です。
内側のwhileループでは、変数tを2からdまで1ずつ増やしながら繰り返しています。変数dの範囲は「2～N」であり、d=2のときは0回、d=3のときは1回、…、d=Nのときは(N－2)回実行されます。この処理の平均実行回数を式で表すと「(0＋N－2)÷2」回となり、整理すると(N÷2－1)回 ⇒ (0.5N－1)回となります。

オーダー記法では、Nを極限に近づけたとき(N→∞)の計算量の増加傾向を簡潔に示すため、Nの係数や定数部分は省略します。そのため、外側のwhileループも内側のwhileループのいずれも計算量はO(N)です。2つのループは入れ子構造となっているので、プログラム全体の計算量は「O(N)×O(N)＝O(N²)」となります。

∴ア＝O(N²)

解説

解説の便宜上、図2のプログラムに行番号を振っておきます。〔イについて〕
空欄イがtrueの場合には、primes の末尾にdの値を追加する処理が行われます。変数 primes は結果となる素数の一覧を格納する配列なので、dの値を素数として追加していることになります。この処理は〔アルゴリズムの改良1〕(2)b.①の「dが素数であることを確定させる」に当たります。dが素数であることを確定するのは「dが"素数である"とマークされている場合」ですから、この条件が空欄イに入るとわかります。

素数であるかどうかの管理は、配列 isPrime で行われています。行2のコメント部より、配列 isPrime は真偽値を要素とする配列で、isPrime[k] がtrueのとき、kが素数であることを表します。現在注目しているdが素数であるかどうかは isPrime[d] を参照して確認します。したがって、dが"素数である"という条件式は「isPrime[d]がtrueと等しい」と表せます。

∴イ＝isPrime[d]がtrueと等しい

〔ウについて〕
図2のプログラムでは、「2以上の自然数sについて，s自身を除くsの正の倍数uは，1とu以外にsも約数に含むので素数ではない」という性質を利用しています。例えば、3が素数であるとわかった場合、3以外の3の倍数（6、9、12…）はもはや素数である可能性はないということです。

空欄ウの処理は、dが素数であることが確定させた後に実行しているので、〔アルゴリズムの改良1〕(2)b.②の「d以上の自然数xについて，dをx倍した数を"素数ではない"とマークする」に当たります。変数 t の初期値は d×d ですので、次々とdの倍数を"素数でない"をマークしていくには、d×d、d×(d＋1)、d×(d＋2)、…というように、マーク対象の要素を変えていくことになります。都度＋1倍とするには、現在の変数 t の値に d を加算することで実現可能ですから、空欄ウには「t＋d」が当てはまります。

【補足】
変数 t の初期値が d×2 ではなく d×d になっているのは、d未満の数の倍数についてはそれまでの処理で既に"素数ではない"とマークされているためです。

∴ウ＝t＋d

解説

解説の便宜上、図3のプログラムに行番号を振っておきます。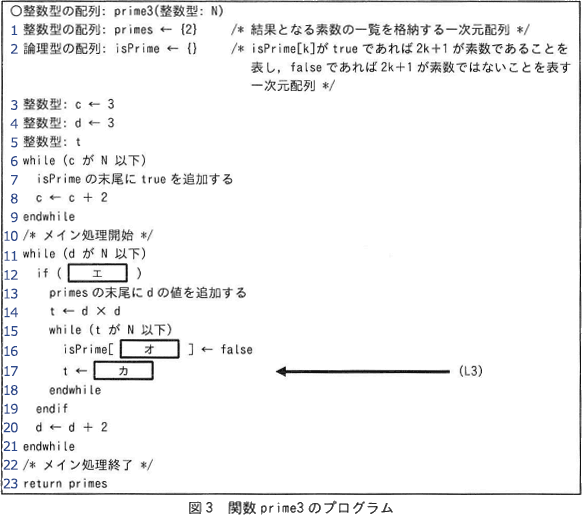〔エについて〕
空欄エには空欄イと同じく、dが"素数である"とマークされている場合にtrueとなる条件式が入れる必要があります。
素数であるかどうかの管理を配列 isPrime で行っていることは図2のプログラムと同じですが、図3では奇数だけを検証対象とするため、isPrime も奇数についてのみ情報を保持するように変更されています。行2のコメント「isPrime[k]がtrueであれば2k＋1が素数であることを表（す）」より、dが2k＋1のとき参照すべき要素は isPrime[k] になることがわかります。具体的には、配列 isPrime に格納される真偽値と値の関係は次のようになります。2k＋1＝d の関係より、dからkを求める式は以下のようになります。

　2k＋1＝d
　2k＝d－1
　k＝(d－1)÷2

参照すべき要素は isPrime[(d－1)÷2] となるので、空欄エには「isPrime[(d－1)÷2]がtrueと等しい」という条件式が当てはまります。

∴エ＝isPrime[(d－1)÷2]がtrueと等しい

〔オについて〕
図2のプログラムと同じく、tの値について"素数でない"とマークする処理です。空欄エの対応関係と同じく、マーク対象の値がtである場合、それに対応する配列 isPrime の要素番号は次の式で表すことができます。

　t＝2k＋1
　2k＝t－1
　k＝(t－1)÷2

したがって、空欄オには「(t－1)÷2」が当てはまります。

∴オ＝(t－1)÷2

〔カについて〕
素数であると判定した場合に、その倍数を"素数でない"とマークすることは図2のプログラムと同じですが、図3のプログラムではいずれのループも奇数についてだけ実行することが異なります。仮に3を素数と判定した場合であれば、3×3、3×5、3×7、…というようにマーク対象の要素を変えていく必要があります。

図2のプログラムでは、現在のtの値にdを加算することで＋1倍を実現していましたが、ここでは＋2倍としたいためdを2倍した値を加算すれば求める処理となります。したがって、空欄カには「t＋2×d」が当てはまります。

∴カ＝t＋2×d

解説

〔L1について〕
設問1の解説で記述したとおり、ループ回数は以下のようになります。

• 外側のwhileループは2～20まで繰り返されるので19回
• 内側のwhileループは、外側のwhileループ1回ごとに(d－2)回

L1は、d=2のとき0回、d=3のとき1回、…、d=20のとき18回実行されるので、

　0＋1＋2＋3＋…＋17＋18＝171

または和の公式 n(n＋1)2 を使って、

　(18×19)÷2＝342÷2＝171

∴171（回）

〔L2について〕
最初に、図2の行12でif条件が真となるdの値を列挙します。
dの初期値は2、N=20なので、2以上20以下の素数である、2、3、5、7、11、13、17が該当します。それぞれの値についてトレースをしてみると、L2が実行される回数は次のようになります。

• d=2　2×3 から 2×11 までの9回
• d=3　3×4 から 3×7 までの4回
• d=5　5×5＝25＞20 なので0回
• 以下、dが7～17まで同様に0回

以上より、L2が実行される回数は「9＋4＝13回」です。

∴13（回）

〔L3について〕
L2と同様に、図3の行12でif条件が真となるdの値を列挙します。
dの初期値は3、N＝20、3以上20以下の素数である、3、5、7、11、13、17が該当します。それぞれのの値についてトレースをしてみると、L3が実行される回数は次のようになります。

• d=3　3×5、3×7の2回
• d=5　5×5＝25＞20 なので0回
• 以下、dが7～17まで同様に0回

以上より、L3が実行される回数は2回です。

∴2（回）