令和7年秋期試験午後問題 問3
問3 プログラミング
⇱問題PDF
二つの列の最長共通部分列(Longest Common Subsequence)の長さを求めるアルゴリズムに関する次の記述を読んで,設問に答えよ。
二つの列の最長共通部分列(Longest Common Subsequence)の長さを求めるアルゴリズムに関する次の記述を読んで,設問に答えよ。
広告
列X={x1,x2,…,xn}に対して,順序を保持して要素を抽出した列を部分列という。また,列の長さはその列の要素の個数で定義される。ここでは,各要素が文字である列を考える。例えば,X={"A","B","C","B","D","A","B"} のとき,図1に示すように{"B","C","D","B"}はXの部分列の例であり,その長さは4である。 ある列Zが二つの列X,Y両方の部分列であるとき,ZをXとYとの共通部分列といい,共通部分列のうち長さが最大となるものを最長共通部分列という。最長共通部分列は複数通り存在する場合もあるが,その長さは一意に決まる。X={"A","B","C","B","D","A","B"},Y={"B","D","C","A","B","A"}の場合の共通部分列及び最長共通部分列の例を図2に示す。
ある列Zが二つの列X,Y両方の部分列であるとき,ZをXとYとの共通部分列といい,共通部分列のうち長さが最大となるものを最長共通部分列という。最長共通部分列は複数通り存在する場合もあるが,その長さは一意に決まる。X={"A","B","C","B","D","A","B"},Y={"B","D","C","A","B","A"}の場合の共通部分列及び最長共通部分列の例を図2に示す。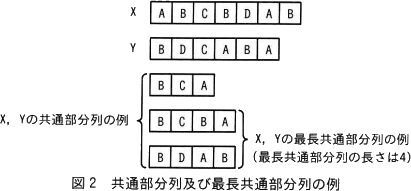 なお,共通部分列が存在しない場合,最長共通部分列は空の列となり,その長さは0である。
なお,共通部分列が存在しない場合,最長共通部分列は空の列となり,その長さは0である。
最長共通部分列の長さは,2本のDNAの塩基配列間の類似度を測る目的などに用いられる。
〔最長共通部分列の長さを求めるアルゴリズム〕
二つの列X,Yの最長共通部分列の長さを求めるアルゴリズムを考える。列X,Yそれぞれについて,先頭からn個,k個の要素を抽出した列をXn,Ykと表記し,列Xn,Ykそれぞれの末尾の要素をxn,ykと表記する。例えば,X={"A","B"}とすると,X3={"A","B","C"},x3="C"である。このとき,列Xnと列Ykとの最長共通部分列の中の一つをLCS(n,k),最長共通部分列の長さをLCSL(n,k)と表記する。なお,X0とY0は空の列であり,x0とy0は存在しない。
ここで,xnとykとが一致しているか否かに着目して次の(1)~(3)に場合分けし,再帰的な関係を用いてLCSL(n,k)を求めることを考える。
(1)~(3)の再帰的な関係に従い,LCSL(n,k)を再帰的に計算することによって,列X,Yの最長共通部分列の長さを求めることができる。しかし,再帰的に計算するアルゴリズムでは,重複して同じ計算をすることによって時間計算量が大きくなり,非効率になる場合がある。そこで,重複して同じ計算をすることを避けるために,LCSL(n,k)の値を動的計画法によって求めることを考える。
二つの列がX={"A","B","C","B","D","A","B"},Y={"B","D","C","A","B","A"} の場合,0≦n≦7かつ0≦k≦6に対するLCSL(n,k)の値を図3に示す。図3の左端2列はn(0~7)とそれに対応するxnを,上端2行はk(0~6)とそれに対応するykを表す。n=0のときのxn,k=0のときのykは存在しないので,"-"と表す。各要素は列Xn,と列Ykとの最長共通部分列の長さLCSL(n,k)の値を示している。 図3の各要素の値は,〔最長共通部分列の長さを求めるアルゴリズム〕の(1)~(3)の再帰的な関係に従って求められる。
図3の各要素の値は,〔最長共通部分列の長さを求めるアルゴリズム〕の(1)~(3)の再帰的な関係に従って求められる。
まず,n=0又はk=0のときは(3)に対応するので,LCSL(n,k)=0である。
それ以外の値について,例えば,図3の①~③は次のように値が決まる。
①について,x2=y1なので(1)に対応し,LCSL(2,1)=LCSL(1,0)+1である。LCSL(1,0)=0なので,LCSL(2,1)=1となる。
②について,x2≠y2なので(2)に対応し,LCSL(2,1)=1,LCSL(1,2)=0なので,LCSL(2,2)=1となる。
③について,X6≠y2なので(2)に対応し,LCSL(6,1)=1,LCSL(5,2)=2なので,LCSL(6,2)=2となる。
図3の要素の値を全て計算することによって列X,Yの最長共通部分列の長さが4であると分かる。
〔動的計画法を用いて最長共通部分列の長さを求めるプログラム〕
〔動的計画法を用いて最長共通部分列の長さを求めるアルゴリズム〕に基づいて,二つの列の最長共通部分列の長さを求めるプログラムを考える。任意の二つの列をそれぞれ配列S,Tとして受け取り,動的計画法を用いて最長共通部分列の長さを求めるプログラムを図4に示す。ここで,配列の要素番号は0から始まり,整数型の二次元配列 lcsl は,行番号が0から配列Sの要素数sまでの(s+1)行,列番号が0から配列Tの要素数tまでの(t+1)列の大きさをもつ。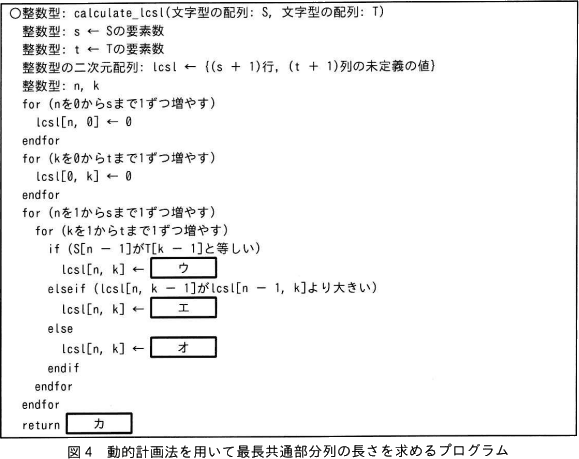 図4のプログラムの時間計算量を,配列Sの要素数s, 配列Tの要素数tを用いて表すとO(キ)である。
図4のプログラムの時間計算量を,配列Sの要素数s, 配列Tの要素数tを用いて表すとO(キ)である。


最長共通部分列の長さは,2本のDNAの塩基配列間の類似度を測る目的などに用いられる。
〔最長共通部分列の長さを求めるアルゴリズム〕
二つの列X,Yの最長共通部分列の長さを求めるアルゴリズムを考える。列X,Yそれぞれについて,先頭からn個,k個の要素を抽出した列をXn,Ykと表記し,列Xn,Ykそれぞれの末尾の要素をxn,ykと表記する。例えば,X={"A","B"}とすると,X3={"A","B","C"},x3="C"である。このとき,列Xnと列Ykとの最長共通部分列の中の一つをLCS(n,k),最長共通部分列の長さをLCSL(n,k)と表記する。なお,X0とY0は空の列であり,x0とy0は存在しない。
ここで,xnとykとが一致しているか否かに着目して次の(1)~(3)に場合分けし,再帰的な関係を用いてLCSL(n,k)を求めることを考える。
- xn=ykの場合を考える。例えば,xn=yk="A"とする。このとき,LCS(n,k)の末尾の要素は"A"となる。よって,LCS(n,k)は,列Xn-1,Yk-1の最長共通部分列LCS(n-1,k-1)の末尾に"A"を付加したものと一致する。したがって,LCSL(n,k)=LCSL(n-1,k-1)+1が成り立つ。
- xn≠ykの場合を考える。例えば,xn="A",yk="B"とする。ここで,LCS(n,k)の末尾の要素は"A"又は"A"以外となる。LCS(n,k)の末尾の要素が"A"である場合は,列Ykから末尾の"B"を取り除いても最長共通部分列には影響しないので,LCS(n,k)はLCS(n,k-1)と一致する。一方,LCS(n,k)の末尾の要素が"A"でない場合は,列Xnから末尾の"A"を取り除いても最長共通部分列には影響しないので,LCS(n,k)はLCS(n-1,k)と一致する。よって,LCS(n,k)はLCS(n,k-1)又はLCS(n-1,k)のいずれかと一致する。したがって,LCSL(n,k)は,LCSL(n,k-1)とLCSL(n-1,k)のうちの最大値と一致する。
- n=0又はk=0の場合,最長共通部分列は空の列となり,LCSL(n,k)=0である。
(1)~(3)の再帰的な関係に従い,LCSL(n,k)を再帰的に計算することによって,列X,Yの最長共通部分列の長さを求めることができる。しかし,再帰的に計算するアルゴリズムでは,重複して同じ計算をすることによって時間計算量が大きくなり,非効率になる場合がある。そこで,重複して同じ計算をすることを避けるために,LCSL(n,k)の値を動的計画法によって求めることを考える。
二つの列がX={"A","B","C","B","D","A","B"},Y={"B","D","C","A","B","A"} の場合,0≦n≦7かつ0≦k≦6に対するLCSL(n,k)の値を図3に示す。図3の左端2列はn(0~7)とそれに対応するxnを,上端2行はk(0~6)とそれに対応するykを表す。n=0のときのxn,k=0のときのykは存在しないので,"-"と表す。各要素は列Xn,と列Ykとの最長共通部分列の長さLCSL(n,k)の値を示している。

まず,n=0又はk=0のときは(3)に対応するので,LCSL(n,k)=0である。
それ以外の値について,例えば,図3の①~③は次のように値が決まる。
①について,x2=y1なので(1)に対応し,LCSL(2,1)=LCSL(1,0)+1である。LCSL(1,0)=0なので,LCSL(2,1)=1となる。
②について,x2≠y2なので(2)に対応し,LCSL(2,1)=1,LCSL(1,2)=0なので,LCSL(2,2)=1となる。
③について,X6≠y2なので(2)に対応し,LCSL(6,1)=1,LCSL(5,2)=2なので,LCSL(6,2)=2となる。
図3の要素の値を全て計算することによって列X,Yの最長共通部分列の長さが4であると分かる。
〔動的計画法を用いて最長共通部分列の長さを求めるプログラム〕
〔動的計画法を用いて最長共通部分列の長さを求めるアルゴリズム〕に基づいて,二つの列の最長共通部分列の長さを求めるプログラムを考える。任意の二つの列をそれぞれ配列S,Tとして受け取り,動的計画法を用いて最長共通部分列の長さを求めるプログラムを図4に示す。ここで,配列の要素番号は0から始まり,整数型の二次元配列 lcsl は,行番号が0から配列Sの要素数sまでの(s+1)行,列番号が0から配列Tの要素数tまでの(t+1)列の大きさをもつ。

広告
設問1
列{"A","C","B","C","D","C"}と列{"C","D","B","D","C","A"}との最長共通部分列の長さを答えよ。
解答例・解答の要点
4
解説
この設問の解説はまだありません。設問2
図3中のア,イに入れる適切な数値を答えよ。
解答例・解答の要点
ア:2
イ:4
イ:4
解説
この設問の解説はまだありません。設問3
図4中のウ~カに入れる適切な字句を答えよ。
解答例・解答の要点
ウ:lcsl[n-1,k-1] + 1
エ:lcsl[n,k-1]
オ:lcsl[n-1,k]
カ:lcsl[s, t]
エ:lcsl[n,k-1]
オ:lcsl[n-1,k]
カ:lcsl[s, t]
解説
この設問の解説はまだありません。設問4
本文中のキに入れる適切な字句を,sとtを用いて答えよ。
解答例・解答の要点
キ:st
解説
この設問の解説はまだありません。
広告