令和7年春期試験午後問題 問3
問3 プログラミング
⇱問題PDF
スライドパズルを解くプログラムに関する次の記述を読んで,設問に答えよ。
スライドパズルを解くプログラムに関する次の記述を読んで,設問に答えよ。
広告
表1のルールで定義されるスライドパズルについて考える。 一辺が3マスのスライドパズルの例を図1に示す。
一辺が3マスのスライドパズルの例を図1に示す。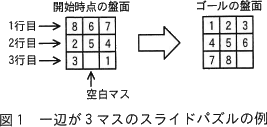 本問では,一辺のマスの個数が任意のスライドパズルにおいて,ゴールの盤面になるまでの駒の移動回数が最小となる移動方法(以下,最小解という)を一つ求めるプログラムを作成する。
本問では,一辺のマスの個数が任意のスライドパズルにおいて,ゴールの盤面になるまでの駒の移動回数が最小となる移動方法(以下,最小解という)を一つ求めるプログラムを作成する。
〔一辺がNマスのスライドパズルの最小解を幅優先探索を用いて求める方法〕
幅優先探索を行ったときの,スライドパズルの盤面の遷移を,グラフで表現する。開始時点の盤面をルートノード,ある時点の盤面をノード,駒の移動に伴う盤面の遷移をエッジで表現する。また,ゴールの盤面をゴールノードとして定義する。
幅優先探索で最小解を求める方法を次のように考える。ここで,Nは2以上とする。
探索対象のノードに対して,移動できる駒ごとにその駒を移動した後のノードを作成して,探索対象のノードの子ノードとし,探索対象のノードは探索済みとなる。このとき,子ノードが表す盤面が既に探索したノード(以下,探索済みノードという)と同じであれば,この子ノードは終端ノードとして,以降の探索は行わない。また,子ノードがゴールノードと同じであれば,最小解が見つかったと判断して探索を終了する。
〔Nが3の場合の例〕
一辺が3マスのスライドパズルの最小解を求める過程の例を図2に示す。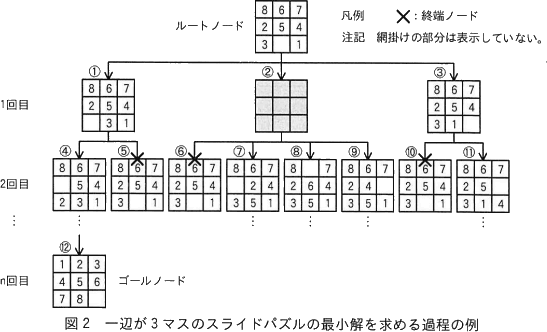
次に,配列を用いた盤面の表現方法を図3に示す。ここで,空白マスを表す値は最も大きい駒の数字である8に1を加えた9とする。なお,配列の要素番号は1から始まるものとする。
〔一辺がNマスのスライドパズルの最小解を求めるプログラム〕
一辺がNマスのスライドパズルにおいて,開始時点の盤面をランダムに作成し,最小解を求め,開始時点の盤面からの遷移及び駒の移動回数を出力するプログラムを作成する。開始時点からの盤面の遷移を保持する単方向連結リストの要素となるクラス BoardState の説明を図4に,キューを実現するクラス Queue の説明を図5に,リストを実現するクラス List の説明を図6に,プログラムで使用する主な関数を表2に,最小解を求めるプログラムを図7に示す。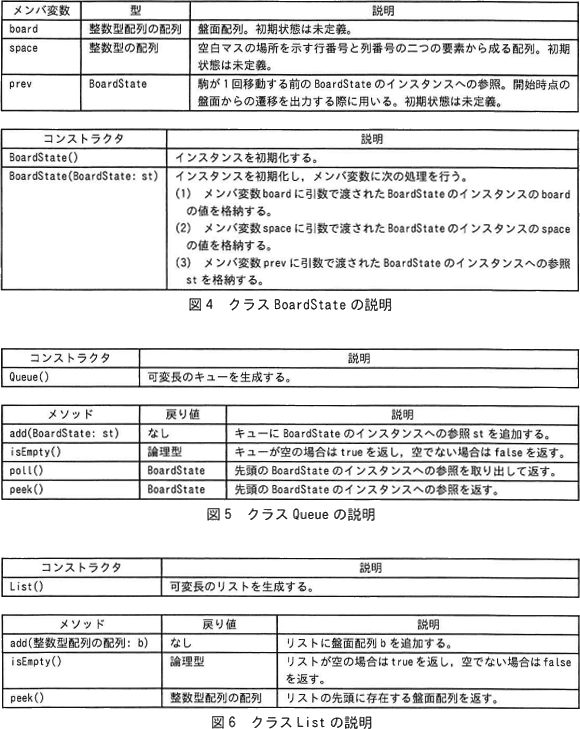



〔一辺がNマスのスライドパズルの最小解を幅優先探索を用いて求める方法〕
幅優先探索を行ったときの,スライドパズルの盤面の遷移を,グラフで表現する。開始時点の盤面をルートノード,ある時点の盤面をノード,駒の移動に伴う盤面の遷移をエッジで表現する。また,ゴールの盤面をゴールノードとして定義する。
幅優先探索で最小解を求める方法を次のように考える。ここで,Nは2以上とする。
探索対象のノードに対して,移動できる駒ごとにその駒を移動した後のノードを作成して,探索対象のノードの子ノードとし,探索対象のノードは探索済みとなる。このとき,子ノードが表す盤面が既に探索したノード(以下,探索済みノードという)と同じであれば,この子ノードは終端ノードとして,以降の探索は行わない。また,子ノードがゴールノードと同じであれば,最小解が見つかったと判断して探索を終了する。
〔Nが3の場合の例〕
一辺が3マスのスライドパズルの最小解を求める過程の例を図2に示す。

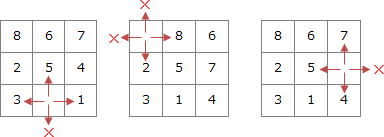
- 1回目の駒の移動では,ルートノードを探索対象のノードとする。ここでは,移動できる駒が三つあるので,ルートノードから深さが1となる①~③の子ノードを作成し,ルートノードは探索済みノードとなる。ここで,①~③の子ノードに対して,ゴールノードの判定及び終端ノードの判定を行う。
- 次に,作成した子ノードで終端ノード以外のノードをそれぞれ探索対象のノードとし,駒の移動にあわせて子ノードを作成する。図2では,①~③のノードから④~⑪の子ノードを作成し,①~③は探索済みノードとなる。ここで,④~⑪の子ノードに対して,ゴールノードの判定及び終端ノードの判定を行う。図2では,盤面が探索済みノードと一致する⑤,⑥及び⑩は終端ノードとなり,以降の探索は行わない。
- 以降,(2)で作成したノードの子ノードの作成と,ゴールノードの判定及び終端ノードの判定を繰り返す。図2の⑫は,n回目の移動でゴールノードに至ったことを示している。なお,全てのリーフノードが終端ノードと判定された場合,ゴールの盤面に至る駒の移動方法がないことを意味しているので,その旨のメッセージを出力して探索を終了する。
次に,配列を用いた盤面の表現方法を図3に示す。ここで,空白マスを表す値は最も大きい駒の数字である8に1を加えた9とする。なお,配列の要素番号は1から始まるものとする。

〔一辺がNマスのスライドパズルの最小解を求めるプログラム〕
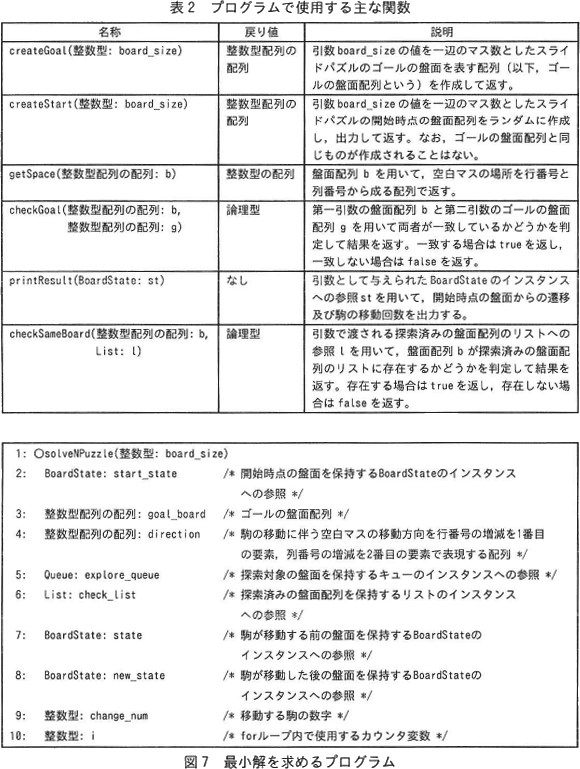
一辺がNマスのスライドパズルにおいて,開始時点の盤面をランダムに作成し,最小解を求め,開始時点の盤面からの遷移及び駒の移動回数を出力するプログラムを作成する。開始時点からの盤面の遷移を保持する単方向連結リストの要素となるクラス BoardState の説明を図4に,キューを実現するクラス Queue の説明を図5に,リストを実現するクラス List の説明を図6に,プログラムで使用する主な関数を表2に,最小解を求めるプログラムを図7に示す。



広告
設問1
図2中の②の盤面を図3に倣って,配列で答えよ。
解答例・解答の要点
{{8,6,7},{2,9,4},{3,5,1}}
解説
問われているのは、図2の②の盤面を図3の規則に従って配列で表すことです。各子ノードは「探索対象のノードに対して,移動できる駒ごとにその駒を移動した後のノード」です。また、図2の作成過程では「1回目の駒の移動では…ルートノードから深さが1となる①~③の子ノードを作成」とあります。つまり、②はルート盤面から空白マスに隣接する駒のどれかを1手だけ動かした盤面です。
ルートノードは中央下の部分が空白マスとなっており、この空白マスに移動可能な駒は左="3"、上="5"、右="1"の3つです。図2中の1回目の3つの盤面のうち、①は"3"を右に移動したもの、③は"1"を左に移動したものに対応しますから、残る②は"5"を下に動かしたケースだとわかります。
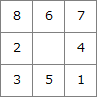

∴{{8,6,7},{2,9,4},{3,5,1}}
広告
設問2
図7中のア~クに入れる適切な字句を答えよ。
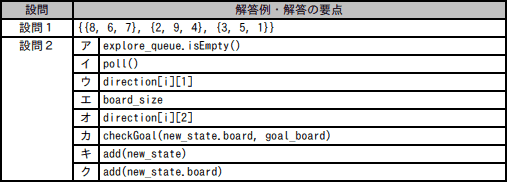
解答例・解答の要点
ア:explore_queue.isEmpty()
イ:poll()
ウ:direction[i] [1]
エ:board_size
オ:direction[i] [2]
カ:checkGoal(new_state.board,goal_board)
キ:add(new_state)
ク:add(new_state.board)
イ:poll()
ウ:direction[i] [1]
エ:board_size
オ:direction[i] [2]
カ:checkGoal(new_state.board,goal_board)
キ:add(new_state)
ク:add(new_state.board)
解説
空欄アにはwhileループを継続するための条件式が入りますが、プログラム全体の流れを把握してからでないと理解しにくいため、説明は最後に回します。〔イについて〕
変数 explore_queue はクラス Queue のインスタンスで、探索対象の盤面データのリストを保持しています。空欄イは.に続く字句なので、ここにはクラス Queue のメソッドかプロパティが入ります。
行21の処理では戻り値をBoardState型変数 state に入れているので、Queueの説明(図5)より、戻り値が適合するpoll()とpeek()が解答の候補となります。どちらもキューの先頭要素への参照を返しますが、poll()が先頭要素を取り出すのに対し、peek()は参照だけで取り出しは行わないという点が異なります。
プログラム全体を見ると、他にキューから取り出す処理が存在しないため、ここで先頭要素が削除されなければ、行21では同じ盤面が繰り返し state に格納されてしまいます。これでは一向に探索処理が進みません。したがって、空欄イには取り出しを伴う「poll()」が当てはまります。
∴イ=poll()
〔ウエオについて〕
空欄を含むif文は、新たな盤面 new_state を作成する際の条件となっています。
本文の動作説明に従うと、子ノードが表す盤面は、空白マスを上下左右のいずれかへ1マス移動することで作成されますが、この際、空白マスの場所によって移動(マス置換え)できる方向が限定されます。
BoardStateの説明(図4)では、盤面における空白マスの位置をメンバ変数 space で保持していることが示されています。space は配列で、[1]が行番号、[2]が列番号です。また、プログラム中では空白マスの移動先の4パターンを保持する変数として、配列 direction が定義されています。行4の説明より、[1]に行番号の増減、[2]に列番号の増減が入っています。
{{1, 0}, {0, -1}, {-1, 0}, {0, 1}} ⇒ 下、左、上、右
この2つのデータを利用すれば境界判定を行うことができます。現在注目している移動パターンは direction[i] で参照できるため、4つある移動パターンの判定を一般化した条件式を考えると、次の4つに整理されます。- space[1] + direction[i][1] が 1 以上(上方向)
- space[1] + direction[i][1] が board_size 以下(下方向)
- space[2] + direction[i][2] が 1 以上(左方向)
- space[2] + direction[i][2] が board_size 以下(右方向)
なお、行27~32行目では、現在探索中の盤面のコピーを new_state に生成(行27)し、空白マスの位置更新(行28、29)、空白マスと移動先マスの要素を入れ替える(行30~32)ことで、子ノードの盤面を作成しています。
∴ウ=direction[i][1]
エ=board_size
オ=direction[i][2]
〔カについて〕
空欄を含むif文がtrueの場合には、関数 printResult により開始時点から盤面の遷移、駒の移動回数を出力され、プログラムは終了しています。本文中の記述と照合すると、これはゴールノードに至った場合の処理であることがわかります。
ゴールノードに至ったかどうかは、表2の関数 checkGoal(b, g) で判定することができます。引数bには「評価対象の盤面」、引数gには「ゴールの盤面配列」を渡します。「評価対象の盤面」には今生成した子ノードの盤面(本文中の「移動できる駒ごとにその駒を移動した後のノード」)である new_state.board を、「ゴールの盤面配列」には行3の createGoal(N) によって生成され保持している goal_board を設定すればよいです。
∴カ=checkGoal(new_state.board,goal_board)
〔キクについて〕
.に続く字句なので、ここにはメソッドかプロパティが入ります。戻り値がなく、すでに両変数は行16、18にてコンストラクタで生成済です。したがって、消去法で add メソッドが入ると判断できます。
本文中ではこの箇所に該当する記述として以下の2つがあります。
- 子ノードが表す盤面が既に探索したノード(探索済みノード)と同じであれば,この子ノードは終端ノードとして,以降の探索は行わない
- 子ノードがゴールノードと同じであれば,最小解が見つかったと判断して探索を終了
空欄に入るメソッド名はいずれも add ですが、クラス Queue の引数 st はBoardState型、クラス List の引数 b は盤面を表す整数配列と異なっています。このため適切な引数は以下のようになります。
- explore_queue.add() ⇒ BoardState型の変数 new_state
- check_list.add() ⇒ そのメンバ変数である new_state.board
∴キ=add(new_state)
ク=add(new_state.board)
〔アについて〕
whileループを抜けた後は、「ゴールの盤面に至る駒の移動方法がない旨のメッセージを出力」してプログラムは終了します。つまり、空欄には探索継続か終了かを判定する条件が入ります。
whileループでは、explore_queue から要素を取り出し、それを基に新たな盤面を生成し、それが終端ノードでなければ explore_queue に追加するという処理を繰り返しています。終端ノードは explore_queue への追加は行われないため、探索が終盤に進むと explore_queue の要素は減っていき、やがて explore_queue は空になります。これが本文中でいう「全てのリーフノードが終端ノードとなった場合」に該当します。
逆にまだ探索対象が存在するうちは、whileループを継続する必要があります。探索対象が存在するかどうかは、クラス Queue の isEmpty() を使って調べられ、isEmpty() がfalse(=空でない)であれば探索を続け、true(=空)になったらwhileループを抜けることになります。したがって、空欄アには「explore_queue.isEmpty()」が当てはまります。
幅優先探索では「探索候補をキューに入れ、キューが空でない間取り出して展開する」という反復が基本となることを覚えておきましょう。
∴ア=explore_queue.isEmpty()
広告
広告