分野 ：テクノロジ系
中分類：基礎理論
小分類：応用数学

長さnの文字列には、n＋1個の境界があります。部分文字列はこの境界から始点と終点を選ぶことによって定義されるため、その種類はn＋1個の境界から2カ所を選ぶ組合せ数と同じくなります。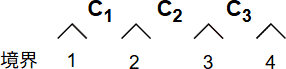異なるN個のものからR個を選ぶ組合せ数は、_NP_RR!の公式で求めることができます。本問ではn＋1個から2個を選ぶため、(n＋1)×n2×1の式となり、これを整理するとn(n＋1)2となります。空文字も種類の1つに数えるとあるため、この式に1を加えた「イ」の式が正解となります。