平成24年秋期試験午後問題 問2
問2 プログラミング
⇱問題PDF
Nクイーン問題に関する次の記述を読んで,設問1~3に答えよ。
Nクイーン問題に関する次の記述を読んで,設問1~3に答えよ。
広告
Nクイーン問題とは,N×Nマスの盤上で互いの利き筋に当たらないようなN個のクイーンの配置を見つける問題である。クイーンは,縦・横・斜めのいずれか一方向にどこまでも移動することができ,一度に移動できる範囲をクイーンの利き筋という。8×8マスの盤上の行5列6に配置したクイーンの利き筋を,図1に示す。また,8×8マスの場合のNクイーン問題の解の一つを図2に示す。
なお,Nクイーン問題の解は存在しないこともあるし,複数存在することもある。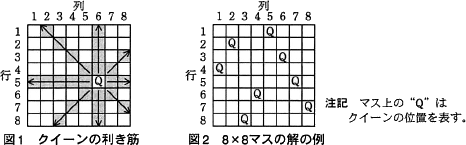 Nクイーン問題に対し,空の盤上にクイーンを配置し,その配置したクイーンの利き筋に当たらない位置を探索しながら,行順にクイーンを配置するという,次のような解法を考えた。
Nクイーン問題に対し,空の盤上にクイーンを配置し,その配置したクイーンの利き筋に当たらない位置を探索しながら,行順にクイーンを配置するという,次のような解法を考えた。
〔Nクイーン問題の解法〕
行 i 列 k のマスが既に配置したクイーンの利き筋に当たるか否かを容易に判別できるよう,盤面の利き筋の方向別に配列 col(列方向),upwd(斜め上方向)及び downwd(斜め下方向)を用意した(図3~5)。解法では,一つの行には一つしかクイーンが配置されないので,行方向の判別は行う必要がない。
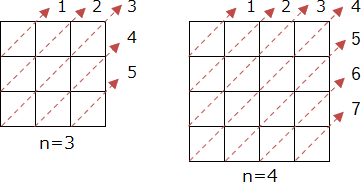
各配列の要素の値は,その方向にまだクイーンが配置されていないとき FREE となり,既に配置されているとき NOT_FREE となる。各要素の初期値は FREE である。図3~5の矢印の先の番号は,各配列の添字に対応する。N×Nマスの場合,配列 col の大きさはNであり,upwd と downwd の大きさはともにアである。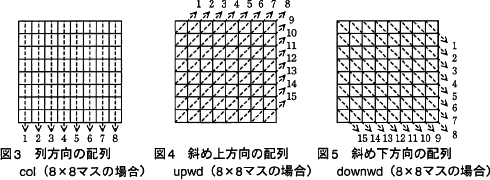 例えば,図6のように8×8マスの盤上の行 1 列 1 と行 2 列 3 のマスにクイーンを配置した場合は,col[1],col[3],upwd[1],upwd[4],downwd[7] 及び downwd[8]の値がNOT_FREEとなる。一般にN×Nマスの盤上の行 i 列 k のマスにクイーンを配置した場合は,col[k],upwd[i+k-1] 及び downwd[イ]の 値がNOT_FREEとなる。
例えば,図6のように8×8マスの盤上の行 1 列 1 と行 2 列 3 のマスにクイーンを配置した場合は,col[1],col[3],upwd[1],upwd[4],downwd[7] 及び downwd[8]の値がNOT_FREEとなる。一般にN×Nマスの盤上の行 i 列 k のマスにクイーンを配置した場合は,col[k],upwd[i+k-1] 及び downwd[イ]の 値がNOT_FREEとなる。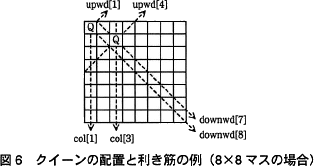 〔Nクイーン問題の解法のプログラム〕
〔Nクイーン問題の解法のプログラム〕
i 行目以降についてクイーンの配置の仕方を探索する再帰関数 search のプログラムを図7に,メインプログラムを図8に示す。 関数 search は i 行目以降のクイーンの配置の仕方が見つかった場合に SUCCESS を,見つからなかった場合に FAILURE を戻す。
配列 pos は,行番号を添字とし,その行に配置したクイーンの位置(列番号)を値とする。配置されていない場合の値は 0 である。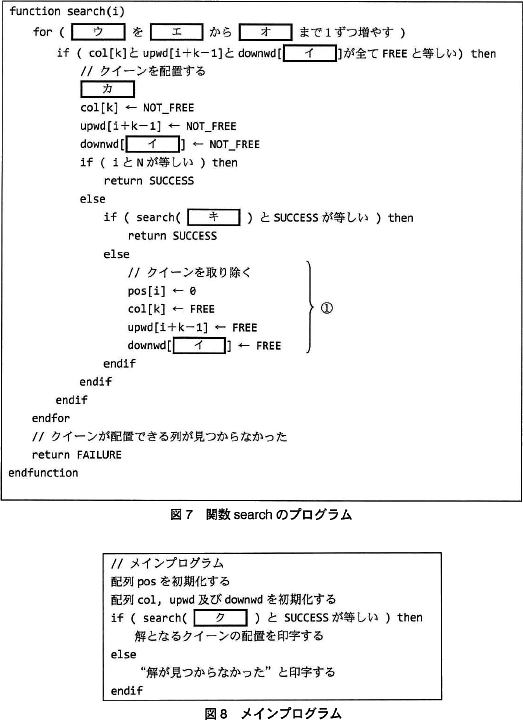
なお,Nクイーン問題の解は存在しないこともあるし,複数存在することもある。

〔Nクイーン問題の解法〕
- 1行目において,1列目にクイーンを配置する。次にこの1行目のクイーンの利き筋に当たらない2行目の列を1列目から順に探索し,クイーンを配置する。同様に次の行以降も,既に配置したクイーンの利き筋に当たらない列を探索し,クイーンを配置する。
- N行目までクイーンが配置できた場合は,解の一つが見つかったとして終了する。
- ある行でクイーンが配置できる列が見つからなかった場合は,一つ前の行に戻り,その行のクイーンを取り除く。取り除いたクイーンの次の列以降で,クイーンが配置できる列を探索する。それでも列が見つからなかった場合は,更に前の行に戻り,同様に繰り返す。
- 1行目においてもクイーンが配置できる列がなくなった場合は,このNクイーン問題の解はないということで終了する。
行 i 列 k のマスが既に配置したクイーンの利き筋に当たるか否かを容易に判別できるよう,盤面の利き筋の方向別に配列 col(列方向),upwd(斜め上方向)及び downwd(斜め下方向)を用意した(図3~5)。解法では,一つの行には一つしかクイーンが配置されないので,行方向の判別は行う必要がない。
各配列の要素の値は,その方向にまだクイーンが配置されていないとき FREE となり,既に配置されているとき NOT_FREE となる。各要素の初期値は FREE である。図3~5の矢印の先の番号は,各配列の添字に対応する。N×Nマスの場合,配列 col の大きさはNであり,upwd と downwd の大きさはともにアである。


i 行目以降についてクイーンの配置の仕方を探索する再帰関数 search のプログラムを図7に,メインプログラムを図8に示す。 関数 search は i 行目以降のクイーンの配置の仕方が見つかった場合に SUCCESS を,見つからなかった場合に FAILURE を戻す。
配列 pos は,行番号を添字とし,その行に配置したクイーンの位置(列番号)を値とする。配置されていない場合の値は 0 である。

広告
設問1
N×Nマスの場合,本文中のアに入れる適切な字句を答えよ。
解答例・解答の要点
ア:2N-1
解説
〔アについて〕N×Nマスの場合の配列 upwd と downwd の大きさが入ります。
N=8のときには本文中の図で示されているように15ですが、Nに別の値を当てはめてみると、例えばN=3のときには5、N=4のときには7となります。この関係をNを使って一般化すると、配列 upwd と downwd の大きさは「2N-1」と表せます。
広告
設問2
N×Nマスの場合,本文及び図7中のイに入れる適切な字句を答えよ。
解答例・解答の要点
イ:i-k+N
解説
〔イについて〕配列 downwd の添字を求める式が入ります。
図5を見ると、左に位置するマスほど、下に位置するマスほど大きな添字になっていることがわかります。図6の downwd[7] および downwd[8]の例だけだと一般化した式が思い付きにくいですが、右上隅のマスと左下隅のマスに注目すると、i、k、添え字に以下の関係があります。
- 右上(i=1, k=8)のマス → 1
- 左下(i=8, k=1)のマス → 15
∴イ=i-k+N
広告
設問3
〔Nクイーン問題の解法のプログラム〕について,(1)~(3)に答えよ。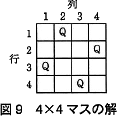
- 図7中のウ~キに入れる適切な字句を答えよ。
- 図8中のクに入れる適切な字句を答えよ。
- 4×4マスの場合,このプログラムによる解を図9に示す。この結果が得られるまでに,図7中の①の部分は何回実行されるか答えよ。

解答例・解答の要点
- ウ:k
エ:1
オ:N
カ:pos[i]←k
キ:i+1
- ク:1
- 4
解説
- 〔ウエオについて〕
クイーンを配置できるマスを探索するための繰返し条件が入ります。
問題文の〔Nクイーン問題の解法〕には、次の記述があります。- 1行目において、1列目にクイーンを配置する。次にこの1行目のクイーンの利き筋に当たらない2行目の列を1列目から順に探索し、クイーンを配置する。同様に次の行以降も、既に配置したクイーンの利き筋に当たらない列を探索し、クイーンを配置する。
∴ウ=k、エ=1、オ=N
〔カについて〕
図7の5行目に、「// クイーンを配置する」とあるため、空欄にはクイーンを配置する処理が当てはまることがわかります。
問題文の〔Nクイーン問題の解放プログラム〕には、クイーンの配置に関して以下の記述があります。- 配列posは、行番号を添字とし,その行に配置したクイーンの位置(列番号)を値とする。配置されていない場合の値は0である。
∴カ=pos[i] ← k
〔キについて〕
関数 search の再帰呼出しを行う際の引数を考えます。
問題文の〔Nクイーン問題の解法〕〔Nクイーン問題の解法のプログラム〕には、以下の記述があります。- …クイーンを配置する。同様に次の行以降も,既に配置したクイーンの利き筋に当たらない列を探索し,クイーンを配置する。
- i行目以降についてクイーンの配置の仕方を探索する再帰関数searchのプログラムを図7に、…に示す。
search(i+1)の呼出し後は、1つ下の行にクイーンが配置できた場合には SUCCESS が、配置できなかった場合には FAILURE が返されます。 FAILURE が返された場合には、復帰後(呼出し元)の関数 search において、列kからクイーンを取り除き、再度 k+1 行目以降のクイーンを配置できるマスを探すことになります。
∴キ=i+1 - 〔クについて〕
〔Nクイーン問題の解法〕にあるように、探索は1行目から始まります。その後、再帰呼出しによって2行目、3行目、…、N行目まで探索が行われる流れになっています。これはNの値が増減しても変わりません。よって、メインプログラムが関数 search を呼び出す際の引数は「1」です。
∴ク=1 - 図7中の①の処理とは、1行下の行にクイーンが配置できなかったときに、呼出し元の行でクイーンを取り除く処理です。4×4マスの場合の探索の様子をトレースすると次のようになります。以下、行i列kを(i, k)と表記しています。
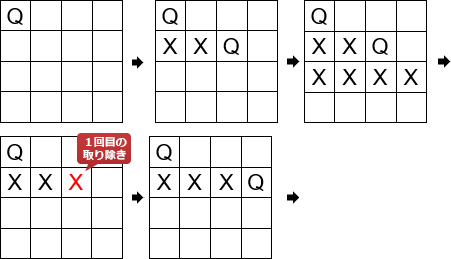
- search(1)
- (1, 1)にクイーンを配置、search(2)を呼び出す
- search(2)
- (2, 3)にクイーンを配置、search(3)を呼び出す
- search(3)
- 配置できる場所がないので、search(2)にFAILUREを返す
- search(2)
- (2, 3)のクイーンを取り除く。(2, 4)にクイーンを配置し、search(3)を呼び出す
- search(3)
- (3, 2)にクイーンを配置、search(4)を呼び出す
- search(4)
- 配置できる場所がないので、search(3)にFAILUREを返す
- search(3)
- (3, 2)のクイーンを取り除く。それ以降配置できる場所がないので、search(2)にFAILUREを返す

- search(2)
- (2, 4)のクイーンを取り除く。それ以降配置できる場所がないので、search(1)にFAILUREを返す
- search(1)
- (1, 1)のクイーンを取り除き、(1, 2)に配置し、search(2)を呼び出す
後は①が実行されることなく4行目までクイーンの配置場所が決まります。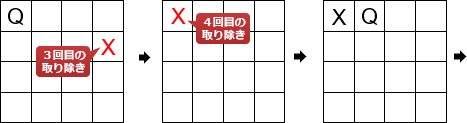
- search(2)
- (2, 4)にクイーンを配置、search(3)を呼び出す
- search(3)
- (3, 1)にクイーンを配置、search(4)を呼び出す
- search(4)
- (4, 3)にクイーンを配置、i=Nとなったので終了
したがって①部分が実行される回数は「4回」です。
∴4
広告

広告