令和7年秋期試験問題 午前問1
問1解説へ
A,B,C,Dを論理変数とするとき,次のカルノー図と等価な論理式はどれか。ここで,・は論理積,+は論理和,XはXの否定を表す。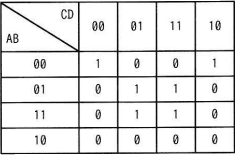

- A・B・C・D+B・D
- A・B・C・D+B・D
- A・B・D+B・D
- A・B・D+B・D
広告
解説
カルノー図は、行・列それぞれの論理変数の組合せの結果が"真"となる場合に"1"を、"偽"となる場合に"0"を、その該当セルに書きこむことで論理式を図式化したものです。論理回路を簡略化するために用いられます。
設問のカルノー図の"1"と"0"、4つの論理変数は下図のように対応します。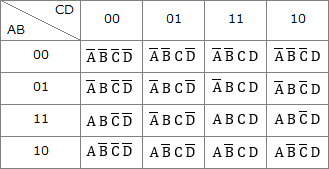 カルノー図から論理式を導くには、図中の値が"1"のセルをグループ化して共通項を取り出すという手順を踏みます。このグループ化は次の4つのルールに従って行います。
カルノー図から論理式を導くには、図中の値が"1"のセルをグループ化して共通項を取り出すという手順を踏みます。このグループ化は次の4つのルールに従って行います。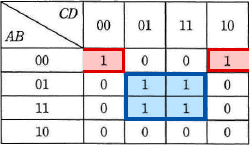 次にグループごとに論理変数の組から共通項を取り出して、その論理積を作ります。
次にグループごとに論理変数の組から共通項を取り出して、その論理積を作ります。
赤枠グループの論理積は「A・B・D」、青枠グループの論理積は「B・D」であり、この2つを論理和(+)でつなぐと「A・B・D+B・D」になります。したがって「エ」が正解です。
設問のカルノー図の"1"と"0"、4つの論理変数は下図のように対応します。

- 値が"1"のセルすべてを長方形で囲むこと
- グループに含まれるセルの数は2n(1, 2, 4, 8, …)であること
- カルノー図の上下左右の端は連続していると考える
- 1つのセルが複数のグループに属してもよい

- 赤枠で囲ったグループ
- 論理変数の組は A B C D と A B C D なので、共通項は A B D、論理積は A・B・D
- 青枠で囲ったグループ
- 論理変数の組は A B C D、A B C D、A B C D、A B C D なので、共通項はB D、論理積はB・D
赤枠グループの論理積は「A・B・D」、青枠グループの論理積は「B・D」であり、この2つを論理和(+)でつなぐと「A・B・D+B・D」になります。したがって「エ」が正解です。
広告