平成18年春期試験問題 午前問5
問5解説へ
x,y,z を論理変数,Tを真,Fを偽とするとき,次の真理値表で示される関数 ƒ(x,y,z) を表す論理式はどれか。ここで∧は論理積,∨は論理和,AはAの否定を表す。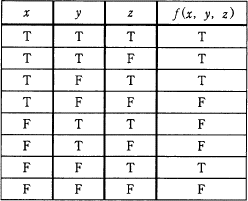

- (x∧y)∨(y∧z)
- (x∧y)∨(y∧z)
- (x∧y)∨(y∧z)
- (x∧y)∨(y∧z)
広告
解説
問題文の真理値表から任意のパターンを選択して各論理式に当てはめていくことで正解を導きます。
なるべくTとFを混じっているパターンを選んだほうが結果が異なりやすいので、最初に「x=T,y=F,z=T,結果T」のパターンを代入してみます。
続いて「x=F,y=F,z=F,結果F」のパターンを試します。
なるべくTとFを混じっているパターンを選んだほうが結果が異なりやすいので、最初に「x=T,y=F,z=T,結果T」のパターンを代入してみます。
- (T∧F)∨(F∧T)=F∨F=F …×
- (T∧F)∨(F∧T)
=(T∧F)∨(T∧T)=F∨T=T …○ - (T∧F)∨(F∧T)
=(T∧F)∨(T∧F)=F∨F=F …× - (T∧F)∨(F∧T)
=(T∧T)∨(T∧F)=T∨F=T …○
続いて「x=F,y=F,z=F,結果F」のパターンを試します。
- 「イ」(F∧F)∨(F∧T)=F∨F=F …○
- 「エ」(F∧F)∨(F∧F)
=(F∧T)∨(T∧T)=F∨T=T …×
広告