分野 ：ストラテジ系
中分類：企業活動
小分類：会計・財務

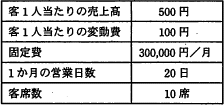
利益は「売上高－費用」で求めることができます。来客数をnとすると、売上と費用はそれぞれ以下のように表すことができます。

• 売上　500n
• 費用　300,000＋100n

月10万円の利益を出すために必要な来客数nは、方程式を使って求めることができます。

　100,000＝500n－(300,000＋100n)
　100,000＝500n－(300,000＋100n)
　100,000＝500n－300,000－100n
　400,000＝400n
　n＝1,000[人]

必要な来客数は1カ月間に1,000人であることがわかります。

1カ月の営業日は20日なので、1日当たりの来客数は「1,000人÷20日＝50人」、席数が10なので1客席当たりの客数は「50人÷10席＝5人」と計算することができます。

したがって正解は「エ」です。

【別解】
損益分岐点売上高を求める計算式の派生で、目標利益を獲得するための売上高を求める式があります。

　目標利益獲得売上高＝(固定費＋目標利益)÷(1－変動費率)

これを使っても求めることが可能です。

　(300,000＋100,000)÷0.8＝500,000[円]
　500,000÷500＝1,000[人]
　1,000[人]÷20[日]÷10[席]＝5[人]