離散数学 (全64問中13問目)
No.13
任意のオペランドに対するブール演算Aの結果とブール演算Bの結果が互いに否定の関係にあるとき,AはBの(又は,BはAの)相補演算であるという。排他的論理和の相補演算はどれか。
出典:平成30年秋期 問1
- [出題歴]
- 応用情報技術者 R3春期 問1
- 応用情報技術者 H24春期 問1
- 基本情報技術者 H14春期 問9
- ソフトウェア開発技術者 H17春期 問3
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ア
解説
相補演算とは、集合演算によって得られる結果が互いにもう一方の演算の補集合となっている関係、すなわちAとA,X AND YとNOT (X AND Y)のような関係になっているものをいいます。
排他的論理和(XOR)は、2つの入力値が異なれば真、同じであれば偽を返す論理演算で、演算結果は次のような真理値表となります。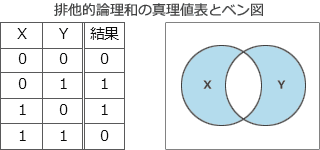 排他的論理和の相補演算になるのは、XORの補集合(XORのベン図の白い部分)が結果として得られる演算なので、答えとして適切なのは「等価演算」ということになります。
排他的論理和の相補演算になるのは、XORの補集合(XORのベン図の白い部分)が結果として得られる演算なので、答えとして適切なのは「等価演算」ということになります。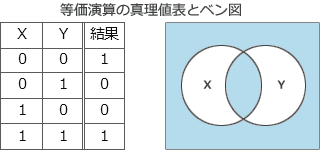
排他的論理和(XOR)は、2つの入力値が異なれば真、同じであれば偽を返す論理演算で、演算結果は次のような真理値表となります。


