HOME»ソフトウェア開発技術者平成20年春期»午前問3
ソフトウェア開発技術者平成20年春期 午前問3
午前問3
浮動小数点形式で表現されたx (x ≫ 1)に対して，√x＋1−√xをそのまま計算すると，けた落ちが生じることがある。それを防ぐために変形した式として，適切なものはどれか。
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ア
解説
けた落ちは、浮動小数点形式で表現された絶対値の非常に近い値同士の減算や、絶対値の近い符号の異なる値同士の加算を行った場合に、計算後の正規化によって有効桁数が少なくなってしまう現象です。
例えば、√10000は100、√10001は100.004999875…ですが、これを有効桁数8桁で計算すると、100.004999875…は100.004999に丸められるので以下のようになります。
100−100.004999＝0.005001 → 5.001×10-3
もともと有効桁数が8桁だったわけですが計算後は4桁に減少しています。このとき浮動小数点形式の仮数部は 50010000 となりますが、後ろ4つの0000の部分は不確かな値です。この不確かな値をもとに乗算などを繰り返すと誤差が大きくなっていきます。これが桁落ちにより誤差です（10進数で説明していますが実際には2進数の計算です）。
この設問では、けた落ちの発生を防ぐために変形した式が正解となるので、けた落ちが発生するかどうかを検討していくことになります。けた落ちが発生するのは、xとxに非常に近い数値の減算があるときですからそれに注目します。
例えば、√10000は100、√10001は100.004999875…ですが、これを有効桁数8桁で計算すると、100.004999875…は100.004999に丸められるので以下のようになります。
100−100.004999＝0.005001 → 5.001×10-3
もともと有効桁数が8桁だったわけですが計算後は4桁に減少しています。このとき浮動小数点形式の仮数部は 50010000 となりますが、後ろ4つの0000の部分は不確かな値です。この不確かな値をもとに乗算などを繰り返すと誤差が大きくなっていきます。これが桁落ちにより誤差です（10進数で説明していますが実際には2進数の計算です）。
この設問では、けた落ちの発生を防ぐために変形した式が正解となるので、けた落ちが発生するかどうかを検討していくことになります。けた落ちが発生するのは、xとxに非常に近い数値の減算があるときですからそれに注目します。
- 正しい。xとxに非常に近い値の加算なので、けた落ちは発生しません。けた落ちを防ぐための方法として"分子の有理化"がありますが、この式は以下のように√x＋1−√xを有理化したものです。
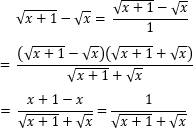
- 仮にxを10000だとすると、
20000＋1−2√10000√10001
＝20001−20000よりわずかに大きい値
となり、絶対値が非常に近い値同士の減算が行われるのでけた落ちが発生します。 - 仮にxを10000だとすると、
√10000√10001(1／√10000−1／√10001)
＝√10000√10001(√10001−√10000)／(√10000√10001))
となり、"√10001−√10000"の部分で絶対値が非常に近い値同士の減算が行われるのでけた落ちが発生します。 - 仮にxを10000だとすると、
(√10000√10001)−10000)／√10000
＝(10000よりわずかに大きい値−10000)／√10000
となり、"10000よりわずかに大きい値−10000"の部分で絶対値が非常に近い値同士の減算が行われるのでけた落ちが発生します。