離散数学 (全64問中11問目)
No.11
0以上255以下の整数nに対して,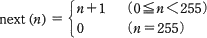 と定義する。next(n)と等しい式はどれか。ここで,x AND y 及び x OR y は,それぞれxとyを2進数表現にして,桁ごとの論理積及び論理和をとったものとする。
と定義する。next(n)と等しい式はどれか。ここで,x AND y 及び x OR y は,それぞれxとyを2進数表現にして,桁ごとの論理積及び論理和をとったものとする。
出典:平成31年春期 問1
- (n+1) AND 255
- (n+1) AND 256
- (n+1) OR 255
- (n+1) OR 256
- [出題歴]
- 応用情報技術者 R5春期 問1
- 応用情報技術者 H22春期 問1
- 応用情報技術者 H27秋期 問1
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ア
解説
next(n)は、引数nが0~254の場合には引数に1を加えた値を返し、255では0を返します。
この問題で考えなければならないポイントは、次の2点です。
この問題で考えなければならないポイントは、次の2点です。
- 1ずつ加算がおこなわれるか。
- next(255)のときに結果が 0 となるか。
- 正しい。ビットマスクの255を2進数で表すと「11111111」で、このビット列との論理積(AND)は(n+1)の下位8ビットだけを取り出すように作用します。引数が255の場合には、最上位ビットの演算結果が0になるので関数は0を返します。
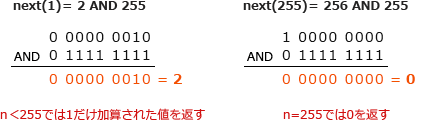
- ビットマスクの256を2進数で表すと「1 00000000」です。どの引数を与えても下位8ビットの演算結果が常に0になってしまうため誤りです。
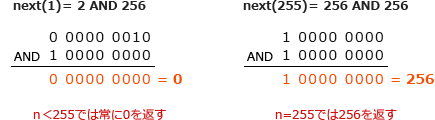
- ビットマスクの255を2進数で表すと「11111111」で、このビット列と論理和(OR)演算を行った結果の下位8ビットは常に「11111111」になります。0≦n<255では常に255、255では511が返るため誤りです。
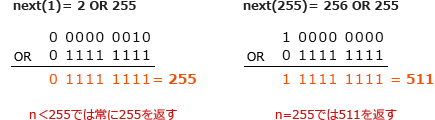
- ビットマスクの256を2進数で表すと「1 00000000」で、このビット列と論理和(OR)演算を行った結果の最上位ビットは常に1になります。どの引数を与えても常に256以上の値が返るため誤りです。

