応用情報技術者過去問題 令和5年秋期 午後問3
⇄問題文と設問を画面2分割で開く⇱問題PDF問3 プログラミング
2分探索木に関する次の記述を読んで,設問に答えよ。
2分探索木とは,木に含まれる全てのノードがキー値をもち,各ノードNが次の二つの条件を満たす2分木のことである。ここで,重複したキー値をもつノードは存在しないものとする。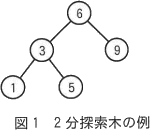 2分探索木をプログラムで表現するために,ノードを表す構造体 Node を定義する。構造体 Node の構成要素を表1に示す。
2分探索木をプログラムで表現するために,ノードを表す構造体 Node を定義する。構造体 Node の構成要素を表1に示す。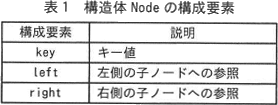 構造体 Node を新しく生成し,その構造体への参照を変数 p に代入する式を次のように書く。
構造体 Node を新しく生成し,その構造体への参照を変数 p に代入する式を次のように書く。
p ← newNode(k)
ここで,引数 k は生成するノードのキー値であり,構成要素 key の初期値となる。構成要素 left 及び right は,参照するノードがないこと(以下,空のノードという)を表すNULLで初期化される。また,生成した p の各構成要素へのアクセスには"."を用いる。例えば,キー値は p.key でアクセスする。
〔2分探索木におけるノードの探索・挿入〕
キー値 k をもつノードの探索は次の手順で行う。
これらの手順によって探索を行う関数 search のプログラムを図2に,挿入を行う関数 insert のプログラムを図3に示す。関数 search は,探索に成功した場合は見つかったノードへの参照を返し,失敗した場合はNULLを返す。関数 insert は,得られた木の根への参照を返す。 関数 search を用いてノードの総数がn個の2分探索木を探索するとき,探索に掛かる最悪の場合の時間計算量(以下,最悪時間計算量というはO(ア)である。これは葉を除く全てのノードについて左右のどちらかにだけ子ノードが存在する場合である。一方で,葉を除く全てのノードに左右両方の子ノードが存在し,また,全ての葉の深さが等しい完全な2分探索木であれば,最悪時間計算量はO(イ)となる。したがって,高速に探索するためには,なるべく左右両方の子ノードが存在するように配置して,高さができるだけ低くなるように構成した木であることが望ましい。このような木のことを平衡2分探索木という。
関数 search を用いてノードの総数がn個の2分探索木を探索するとき,探索に掛かる最悪の場合の時間計算量(以下,最悪時間計算量というはO(ア)である。これは葉を除く全てのノードについて左右のどちらかにだけ子ノードが存在する場合である。一方で,葉を除く全てのノードに左右両方の子ノードが存在し,また,全ての葉の深さが等しい完全な2分探索木であれば,最悪時間計算量はO(イ)となる。したがって,高速に探索するためには,なるべく左右両方の子ノードが存在するように配置して,高さができるだけ低くなるように構成した木であることが望ましい。このような木のことを平衡2分探索木という。
〔2分探索木における回転操作〕
2分探索木中のノード X と X の左側の子ノード Y について,X を Y の右側の子に,元の Y の右側の部分木を X の左側の部分木にする変形操作を右回転といい,逆の操作を左回転という。回転操作後も2分探索木の条件は維持される。木の回転の様子を図4に示す。ここで,t1~t3 は部分木を表している。また,根から t1~t3 の最も深いノードまでの深さを,図4(a)では d1~d3,図4(b)では d1'~d3' でそれぞれ表している。ここで,d1'=d1-1,d2'=d2,d3'=d3+1,が成り立つ。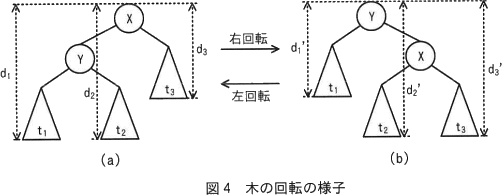 右回転を行う関数 rotateR のプログラムを図5に,左回転を行う関数 rotateL のプログラムを図6に示す。これらの関数は,回転した結果として得られた木の根への参照を返す。
右回転を行う関数 rotateR のプログラムを図5に,左回転を行う関数 rotateL のプログラムを図6に示す。これらの関数は,回転した結果として得られた木の根への参照を返す。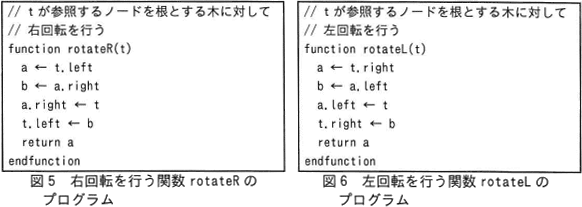 〔回転操作を利用した平衡2分探索木の構成〕
〔回転操作を利用した平衡2分探索木の構成〕
全てのノードについて左右の部分木の高さの差が1以下という条件(以下,条件Balという)を考える。条件Balを満たす場合,完全ではないときでも比較的左右均等にノードが配置された木になる。
条件Balを満たす2分探索木 W に対して図3の関数 insert を用いてノードを挿入した2分探索木を W' とすると,ノードが挿入される位置によっては左右の部分木の高さの差が2になるノードが生じるので,W' は条件Balを満たさなくなることがある。その場合,挿入したノードから根まで,親をたどった各ノード T に対して順に次の手順を適用することで,条件Balを満たすように W' を変形することができる。 条件Balを満たすノードの総数がn個の2分探索木に対して関数 insertB を実行した場合,挿入に掛かる最悪時間計算量はO(キ)となる。
条件Balを満たすノードの総数がn個の2分探索木に対して関数 insertB を実行した場合,挿入に掛かる最悪時間計算量はO(キ)となる。
2分探索木とは,木に含まれる全てのノードがキー値をもち,各ノードNが次の二つの条件を満たす2分木のことである。ここで,重複したキー値をもつノードは存在しないものとする。
- Nの左側の部分木にある全てのノードのキー値は,Nのキー値よりも小さい。
- Nの右側の部分木にある全てのノードのキー値は,Nのキー値よりも大きい。


p ← newNode(k)
ここで,引数 k は生成するノードのキー値であり,構成要素 key の初期値となる。構成要素 left 及び right は,参照するノードがないこと(以下,空のノードという)を表すNULLで初期化される。また,生成した p の各構成要素へのアクセスには"."を用いる。例えば,キー値は p.key でアクセスする。
〔2分探索木におけるノードの探索・挿入〕
キー値 k をもつノードの探索は次の手順で行う。
- 探索対象の2分探索木の根を参照する変数を t とする。
- t が空のノードであるかを調べる。
(2-1) t が空のノードであれば,探索失敗と判断して探索を終了する。
(2-2) t が空のノードでなければ,t のキー値 t.key と k を比較する。- t.key=k の場合,探索成功と判断して探索を終了する。
- t.key>k の場合,t の左側の子ノードを新たな t として(2)から処理を行う。
- t.key<k の場合,t の右側の子ノードを新たな t として(2)から処理を行う。
これらの手順によって探索を行う関数 search のプログラムを図2に,挿入を行う関数 insert のプログラムを図3に示す。関数 search は,探索に成功した場合は見つかったノードへの参照を返し,失敗した場合はNULLを返す。関数 insert は,得られた木の根への参照を返す。

〔2分探索木における回転操作〕
2分探索木中のノード X と X の左側の子ノード Y について,X を Y の右側の子に,元の Y の右側の部分木を X の左側の部分木にする変形操作を右回転といい,逆の操作を左回転という。回転操作後も2分探索木の条件は維持される。木の回転の様子を図4に示す。ここで,t1~t3 は部分木を表している。また,根から t1~t3 の最も深いノードまでの深さを,図4(a)では d1~d3,図4(b)では d1'~d3' でそれぞれ表している。ここで,d1'=d1-1,d2'=d2,d3'=d3+1,が成り立つ。


全てのノードについて左右の部分木の高さの差が1以下という条件(以下,条件Balという)を考える。条件Balを満たす場合,完全ではないときでも比較的左右均等にノードが配置された木になる。
条件Balを満たす2分探索木 W に対して図3の関数 insert を用いてノードを挿入した2分探索木を W' とすると,ノードが挿入される位置によっては左右の部分木の高さの差が2になるノードが生じるので,W' は条件Balを満たさなくなることがある。その場合,挿入したノードから根まで,親をたどった各ノード T に対して順に次の手順を適用することで,条件Balを満たすように W' を変形することができる。
- T の左側の部分木の高さが T の右側の部分木の高さより2大きい場合
T を根とする部分木に対して右回転を行う。ただし,T の左側の子ノード U について,U の右側の部分木の方が U の左側の部分木よりも高い場合は,先に U を根とする部分木に対して左回転を行う。 - T の右側の部分木の高さが T の左側の部分木の高さより2大きい場合
T を根とする部分木に対して左回転を行う。ただし,T の右側の子ノード V について,V の左側の部分木の方が V の右側の部分木よりも高い場合は,先に V を根とする部分木に対して右回転を行う。

設問1
本文中のア,イに入れる適切な字句を答えよ。
解答入力欄
- ア:
- イ:
解答例・解答の要点
- ア:n
- イ:log n
解説
最悪時間計算量とは、そのアルゴリズムにおいて所要時間が最大の場合の計算量のことをいいます。本文中で「ノードの総数がn個の2分探索木を探索するとき」とあるので、関数 search の計算量がノードの総数nの大小によってどう変わるかを考えていきます。
まず、関数 search の計算量について確認します。図2のプログラムの再帰呼出し処理を除くと、関数 search のステップ数はnの大小によって変わりません。したがって、関数 search が1回のみ呼び出され、かつ再帰呼び出しをしなかった場合の最悪計算量は O(1) です。
〔アについて〕
「葉を除く全てのノードについて左右のどちらかにだけ子ノードが存在する場合」とは、例えば次のような木です。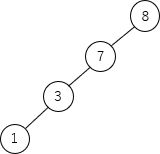 このような木で最悪の計算量となるのは、存在しないキー値を探索して葉までたどった場合です。関数 search は、1つの節について1回呼ばれるので、仮にキー値5のノードを検索すると以下の手順で探索が行われます。
このような木で最悪の計算量となるのは、存在しないキー値を探索して葉までたどった場合です。関数 search は、1つの節について1回呼ばれるので、仮にキー値5のノードを検索すると以下の手順で探索が行われます。
(n+1) × O(1) = O(n+1)
オーダ記法では定数項は無視するので、空欄アには「n」が当てはまります。
∴ア=n
〔イについて〕
「全ての葉の深さが等しい完全な2分探索木」とは、例えば次のような木で、完全2分木と呼ばれます。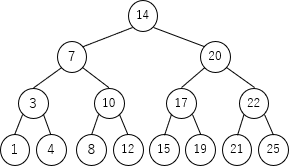 最悪の計算量は、先程と同じく存在しないキー値を探索して葉までたどった場合で(木の高さ+1)回の探索が必要となります。仮にキー値5のノードを検索すると以下の手順で探索が行われます。
最悪の計算量は、先程と同じく存在しないキー値を探索して葉までたどった場合で(木の高さ+1)回の探索が必要となります。仮にキー値5のノードを検索すると以下の手順で探索が行われます。
(log2(n+1)+1) × O(1) = O(log2(n+1)+1)
オーダ記法では対数の底と定数項は無視するので、空欄イには「log n」が当てはまります。
∴イ=log n
まず、関数 search の計算量について確認します。図2のプログラムの再帰呼出し処理を除くと、関数 search のステップ数はnの大小によって変わりません。したがって、関数 search が1回のみ呼び出され、かつ再帰呼び出しをしなかった場合の最悪計算量は O(1) です。
〔アについて〕
「葉を除く全てのノードについて左右のどちらかにだけ子ノードが存在する場合」とは、例えば次のような木です。

- search(ノード8, 5)
- search(ノード7, 5)
- search(ノード3, 5)
- search(ノード1, 5)
- search(null, 5)
(n+1) × O(1) = O(n+1)
オーダ記法では定数項は無視するので、空欄アには「n」が当てはまります。
∴ア=n
〔イについて〕
「全ての葉の深さが等しい完全な2分探索木」とは、例えば次のような木で、完全2分木と呼ばれます。

- search(ノード14, 5)
- search(ノード7, 5)
- search(ノード3, 5)
- search(ノード4, 5)
- search(null, 5)
(log2(n+1)+1) × O(1) = O(log2(n+1)+1)
オーダ記法では対数の底と定数項は無視するので、空欄イには「log n」が当てはまります。
∴イ=log n
設問2
〔回転操作を利用した平衡2分探索木の構成〕について答えよ。
- 図7中のウ~カに入れる適切な字句を答えよ。
- 図1の2分探索木の根を参照する変数を r としたとき,次の処理を行うことで生成される2分探索木を図示せよ。2分探索木は図1に倣って表現すること。
insertB(insertB(r,4),8) - 本文中のキに入れる適切な字句を答えよ。なお,図7中の関数 height の処理時間は無視できるものとする。
解答入力欄
- ウ:
- エ:
- オ:
- カ:
- (図表で回答する問題のため解答入力欄はありません。)
解答例・解答の要点
- ウ:h1が2と等しい
- エ:height(t.left.right) - height(t.left.left)
- オ:h1が-2と等しい
- カ:height(t.right.left) - height(t.right.right)
- log n
解説
- 解説の便宜上、図7のプログラムに行番号を振っておきます。図7のプログラムは〔回転操作を利用した平衡2分探索木の構成〕を実装したものなので、(1)(2)の記述を踏まえて空欄に入る字句を考えていきます。前提として、図7内で記述されているいくつかの表現について本文を確認すると、以下のことがわかります。

- 関数 balance は〔回転操作を利用した平衡2分探索木の構成〕の手順(1)(2)によって木を変形する
- この関数の引数 t は変形したい部分木の根となるノードで、表1で示されている構造体 Node への参照
- 構造体 Node の構成要素より、t.left は t の左側の子ノード、t.right は t の右側の子ノードを指す
- 関数 height(t) は、tが参照するノードを根とする木の高さを返す
- 関数 rotateR(t) は、tが参照するノードを根とする木に対して右回転を行う
- 関数 rotateL(t) は、tが参照するノードを根とする木に対して左回転を行う
if文の内部で、左部分木に対して左回転を行っていること(8行目)、その後、対象となる部分木に対して右回転を行っていること(10行目)から手順(1)に相当する処理であることがわかります。プログラムの5~10行目の処理と手順(1)を比較すると、- 空欄ウの条件式は、Tの左側の部分木の高さがTの右側の部分木の高さより2大きい場合
- 空欄エの条件式は、Tの左側の子ノードUについて、Uの右側の部分木の方がUの左側の部分木よりも高い場合
4行目の処理で変数 h1 には「Tの左側の部分木の高さ-Tの右側の部分木の高さ」が格納されているので、空欄ウの条件式をh1を用いて表すと h1が2が等しい となります。
7行目で「h2が0より大きい」ことを条件としているので、変数 h2 には、Tの左側の子ノードについて「右部分木の高さ-左部分木の高さ」を示す値が格納されている必要があります。左の子ノードの右部分木は t.left.right、左の子ノードの左部分木は t.left.left で参照することができます。部分木の高さは height() で求めることができるため、2つの部分木の高さの差は、- 左の子ノードの右部分木の高さ height(t.left.right)
- 左の子ノードの左部分木の高さ height(t.left.left)
- 2つの部分木の高さの差 height(t.left.right) - height(t.left.left)
∴ウ=h1が2と等しい
エ=height(t.left.right) - height(t.left.left)
〔オカについて〕
if文の内部で、右部分木に対して右回転を行っていること(14行目)、その後、対象となる部分木に対して左回転を行っていること(16行目)から手順(2)に相当する処理です。プログラムの11~16行目の処理と手順(1)を比較すると、- 空欄オの条件式は、Tの右側の部分木の高さが Tの左側の部分木の高さより2大きい場合
- 空欄カの条件式は、Tの右側の子ノードVについて,Vの左側の部分木の方がVの右側の部分木よりも高い場合
変数 h1 は「Tの左側の部分木の高さ-Tの右側の部分木との高さ」なので、右部分木の方が高い場合には値は負数となり、右部分木の高さが2大きい場合には、h1は-2になっているはずです。したがって、空欄オには h1が-2と等しい が当てはまります。
13行目で「h3が0より大きい」ことを条件としているので、変数 h3 には、Tの右側の子ノードについて「左部分木の高さ-右部分木の高さ」を示す値が格納されている必要があります。先程と同様に考えると、空欄カに当てはまる式は、- 右の子ノードの左部分木の高さ height(t.right.left)
- 右の子ノードの右部分木の高さ height(t.right.right)
- 2つの部分木の高さの差 height(t.right.left) - height(t.right.right)
カ=height(t.right.left) - height(t.right.right) - 関数 insertB は、通常のノード挿入をした後に関数 balance によって平衡2分探索木の構成を行います。つまり、insertB(insertB(r,4),8) を実行すると大きく考えて次の4つの処理が行われます。なお、挿入処理の詳細は省略しますが、対象のノードは2分探索木の条件を満たす適切な位置に挿入されます。
- ノード4の挿入
- ノード4の親ノードを始点とする平衡2分探索木の再構成
- ノード8の挿入
- ノード8の親ノードを始点とする平衡2分探索木の再構成
その後、ノード4の親ノードである5を始点として根ノードまでのノードを対象として関数 balance が実行されます。balance(ノード5)及びbalance(ノード3)は、左右の部分木の高さの差が2未満なので何も処理は行われません。次の balance(ノード6) では、左部分木の高さが3、右部分木の高さが1となり、左の部分木の高さが2大きい(h1=2)ので手順(1)の処理対象となります。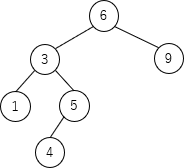
手順(1)の判定式に当てはめてみると、左側の子ノード3について、右部分木の高さ(=2)が左部分木の高さ(=1)よりも高いので、ノード3を根とする部分木が左回転の対象となります。左回転は、右の子ノードを根とし、根としたノードの左部分木を(2分探索木の条件を満たす)適切な位置に移動する処理なので、rotateL(ノード3) では以下の2つの操作が行われます。- ノード3の右の子ノードであるノード5を根とする
- ノード5の左部分木をノード3の右部分木とする
続いて、ノード6を対象とする右回転が実行されます。右回転は、左の子ノードを根とし、根としたノードの右部分木を(2分探索木の条件を満たす)適切な位置に移動する処理なので、rotateR(ノード6) では以下の2つの操作が行われます。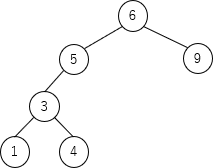
- ノード6の左の子ノードであるノード5を根とする
- ノード5の右部分木をノード6の左部分木とする(※右部分木はないので操作は行われません)
ここまでが、insertB(r, 4) で行われる処理です。関数 balance は、回転で根となったノードの参照を返すので、balance(ノード6) はノード5への参照を返し、これが、insertB(r, 4) の戻り値となります。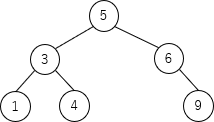
次に、上記の木に対して insertB(ノード5, 8) を実行します。キー値8は6より大きく9より小さいので、再帰呼出しを経てノード9の左の子として挿入されます。その後、ノード8の親ノードである9を始点として根ノードまでのノードを対象として関数 balance が実行されます。balance(ノード9) は、左右の部分木の高さの差が2未満なので何も処理は行われません。次の balance(ノード6) では、左部分木の高さが0、右部分木の高さが2となり、右部分木の高さが2大きい(h1=-2)ので手順(2)の処理対象となります。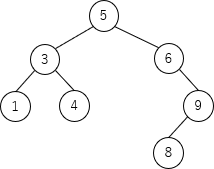
手順(2)の判定式に当てはめてみると、右側の子ノード9について、左部分木の高さ(=1)が右部分木の高さ(=0)よりも高いので、ノード9を根とする部分木が右回転の対象となります。rotateR(ノード9) により、ノード9の左の子ノードであるノード8が根になるので、木は次のようになります。続いて、ノード6を対象とする左回転が実行されます。rotateL(ノード6) により、ノード6の右の子ノードであるノード8が根になるので、木は次のようになります。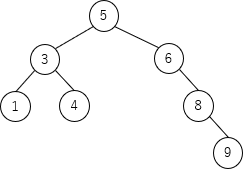 次の balance(ノード5) は、左右の部分木の高さの差が2未満なので何も処理は行われません。
次の balance(ノード5) は、左右の部分木の高さの差が2未満なので何も処理は行われません。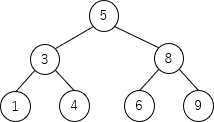
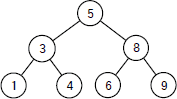
ここまでが、insertB(5, 8) で行われる処理です。関数 balance は、回転で根となったノードの参照を返すので、balance(ノード5) はノード5への参照を返し、これが、insertB(5, 8) の戻り値となります。
∴
- 図8のプログラムより以下のことがわかります。
- 関数 insertB は再帰呼出しされることがある
- 関数 insertB を1回実行すると、関数 balance が1回実行される
次に、関数 insertB の実行回数を考えます。最悪時間計算量を求めるので、実行回数が最大になる場合を想定すると、木の根を基準とする挿入で、最も深い葉にたどり着くまで挿入できなかった場合がこれに該当し、その時の計算量は(木の最大の高さ+1)回となります。
今回扱っている木は「条件 Bal を満たすノードの総数がn個の2分探索木」です。このような木はAVL木(平衡木)と呼ばれ、各葉の深さの差が1以下に保たれていることが特徴です。形状的には完全2分木に近いものですから、AVL木において、ノードの総数がn個であるときの木の最大の高さは log2n(小数点以下切上げ、以下同じ)となり、この場合の関数 insertB の最大実行回数は (log2n+1) 回となります。O(1)の関数 insertB が (log2n+1) 回実行されるので、計算量は以下のように表せます。
(log2n+1) × O(1) = O(log2n+1)
オーダ記法では対数の底と定数項は無視するので、空欄キには「log n」が当てはまります。