応用情報技術者過去問題 平成29年秋期 午後問3
⇄問題文と設問を画面2分割で開く⇱問題PDF問3 プログラミング
ナップザック問題に関する次の記述を読んで,設問1~3に答えよ。
〔ナップザック問題〕
幾つかの種類の品物があり,それぞれの容積と価値が与えられているとき,選んだ品物の容積の合計が定められた値以下であるという条件(容量制限)を満たし,かつ,価値の合計(以下,価値合計という)が最大になるような品物の組合せを求める問題をナップザック問題という。
この問題では,一つの品物を選ぶ個数には制限がないものとする。
例えば,容積,価値を表1に示した2種類の品物A,Bがあり,容量制限が5である問題を考える。この場合,品物Aを1個,品物Bを2個選ぶと,容積の合計は5,価値合計は14となり,選んだ品物の価値合計が最大となる。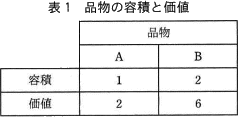 〔動的計画法によるナップザック問題の解法〕
〔動的計画法によるナップザック問題の解法〕
品物の容積や価値を正の整数に限定したナップザック問題に対して,動的計画法による解法が知られている。この問題に対する動的計画法は,元の容量制限以下の全ての値を容量制限としたときの,品物の種類を限定した問題(以下,小問題という)をあらかじめ解いておき,それらの解を用いることによって,元の問題の解を得る方法である。表2に示すような,選んだ品物の最大の価値合計を求める表に対して順に数値を埋めて考えると,この解法の手順は理解しやすい。 表2において,例えば,表1に示す品物A,Bを選べる場合の容量制限3までの小問題が解けているとする。この状態で,容量制限が4で品物A,Bを選べる場合の解は,次の考え方で求めることができる。
表2において,例えば,表1に示す品物A,Bを選べる場合の容量制限3までの小問題が解けているとする。この状態で,容量制限が4で品物A,Bを選べる場合の解は,次の考え方で求めることができる。
容量制限4の場合に最後に品物Bを選んだように,各容量制限の小問題を解いたときに最後に選んだ品物を表3に示す。 容量制限5では,最後に品物Bを選んだことが分かる。次に,品物Bの容積を引いた容量制限3では,最後に品物Bを選んでいる。これを続けていくと,価値合計14を実現する品物の組合せは,品物Aが1個,品物Bが2個であることが分かる。
容量制限5では,最後に品物Bを選んだことが分かる。次に,品物Bの容積を引いた容量制限3では,最後に品物Bを選んでいる。これを続けていくと,価値合計14を実現する品物の組合せは,品物Aが1個,品物Bが2個であることが分かる。
表1の問題に対して,新たに,容積が3で価値が9である品物Cが追加されたときの問題を解くには,表2に品物A,B,Cを選べる場合の行を追加した表4を順に埋めていけばよい。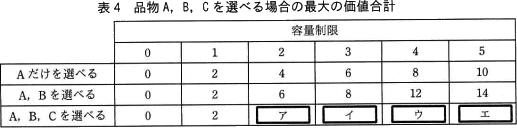 〔ナップザック問題に対する動的計画法によるプログラム〕
〔ナップザック問題に対する動的計画法によるプログラム〕
ナップザック問題に対する動的計画法によるプログラムを図1に示す。なお,Vはナップザックの容量制限,Nは品物の種類の数である。種類s(0~N-1)の品物の容積と価値は,それぞれ,size[s],value[s] に格納されている。また,maxvalue[t]は,容量制限tの小問題の価値合計を保持する配列である。choice[t]は,容量制限tの小問題を解いたときに最後に選んだ品物を保持するための配列である。この配列は,選んだ品物の組合せを最後に出力するために使用する。なお,全ての配列の添字は0から始まる。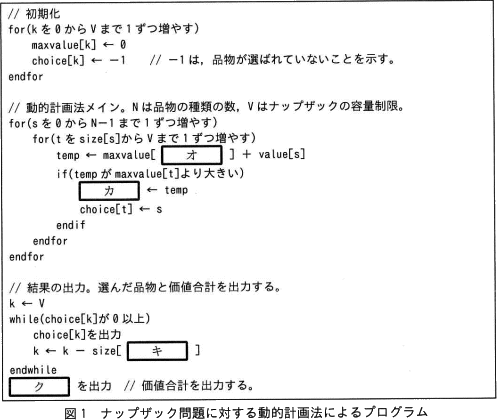 〔計算量に関する検討〕
〔計算量に関する検討〕
動的計画法を用いてナップザック問題を解く場合の計算量のオーダーは,品物の種類の数をN,ナップザックの容量制限をVとすると,O(ケ)である。
〔ナップザック問題〕
幾つかの種類の品物があり,それぞれの容積と価値が与えられているとき,選んだ品物の容積の合計が定められた値以下であるという条件(容量制限)を満たし,かつ,価値の合計(以下,価値合計という)が最大になるような品物の組合せを求める問題をナップザック問題という。
この問題では,一つの品物を選ぶ個数には制限がないものとする。
例えば,容積,価値を表1に示した2種類の品物A,Bがあり,容量制限が5である問題を考える。この場合,品物Aを1個,品物Bを2個選ぶと,容積の合計は5,価値合計は14となり,選んだ品物の価値合計が最大となる。

品物の容積や価値を正の整数に限定したナップザック問題に対して,動的計画法による解法が知られている。この問題に対する動的計画法は,元の容量制限以下の全ての値を容量制限としたときの,品物の種類を限定した問題(以下,小問題という)をあらかじめ解いておき,それらの解を用いることによって,元の問題の解を得る方法である。表2に示すような,選んだ品物の最大の価値合計を求める表に対して順に数値を埋めて考えると,この解法の手順は理解しやすい。

- 容量制限が4で品物Aだけを選べる小問題の解は,表2から8であることが分かる(下線①部分)。
- 品物A,Bを選べる場合,品物Bの容積が2であるので,4から2を減じた容量制限2で品物A,Bを選べる小問題の価値合計6(下線②部分)に,品物Bの価値6を加えた12の価値合計を得られることが分かる。
- 8と12を比較し,大きい方の12を,容量制限4の場合の価値合計として表2に記入する。これは,最後に品物Bを選んだことを意味する。
容量制限4の場合に最後に品物Bを選んだように,各容量制限の小問題を解いたときに最後に選んだ品物を表3に示す。

表1の問題に対して,新たに,容積が3で価値が9である品物Cが追加されたときの問題を解くには,表2に品物A,B,Cを選べる場合の行を追加した表4を順に埋めていけばよい。

ナップザック問題に対する動的計画法によるプログラムを図1に示す。なお,Vはナップザックの容量制限,Nは品物の種類の数である。種類s(0~N-1)の品物の容積と価値は,それぞれ,size[s],value[s] に格納されている。また,maxvalue[t]は,容量制限tの小問題の価値合計を保持する配列である。choice[t]は,容量制限tの小問題を解いたときに最後に選んだ品物を保持するための配列である。この配列は,選んだ品物の組合せを最後に出力するために使用する。なお,全ての配列の添字は0から始まる。

動的計画法を用いてナップザック問題を解く場合の計算量のオーダーは,品物の種類の数をN,ナップザックの容量制限をVとすると,O(ケ)である。
設問1
品物A,B,Cを選べる問題について,〔動的計画法によるナップザック問題の解法〕に従って,(1),(2)に答えよ。
- 表4中のア~エに入れる適切な数値を答えよ。
- 容量制限が5の場合に最大の価値合計を実現する品物A,B,Cそれぞれの個数を答えよ。
解答入力欄
- ア:
- イ:
- ウ:
- エ:
- A:
- B:
- C:
解答例・解答の要点
- ア:6
- イ:9
- ウ:12
- エ:15
- A:0
- B:1
- C:1
解説
- 設問の指示に従って空欄に入る数を計算していきます。
〔アについて〕
容量制限が2、品物Cの容積は3なので、このケースではCの入る余地はありません。したがってアには容量制限が2で、A,Bを選べる場合の合計価値である6が入ります。
〔イについて〕
容量制限が3、品物Cの容積は3なので、対象となる容量制限は3から3を減じた0になります。容量制限0でA,Bを選べる場合の最大価値は0で、これに品物Cを加えたときの価値合計は9になります。容量制限3でA,Bを選べる場合の最大価値は8ですから、イには9と8を比較してより大きい値である9が入ります。
〔ウについて〕
容量制限が4、品物Cの容積は3なので、対象となる容量制限は4から3を減じた1になります。容量制限1でA,Bを選べる場合の最大価値は2で、これに品物Cを加えたときの価値合計は11になります。容量制限4でA,Bを選べる場合の最大価値は12ですから、イには11と12を比較してより大きい値である12が入ります。
〔エについて〕
容量制限が5、品物Cの容積は3なので、対象となる容量制限は5から3を減じた2になります。容量制限2でA,Bを選べる場合の最大価値は6で、これに品物Cを加えたときの価値合計は15になります。容量制限5でA,Bを選べる場合の最大価値は14ですから、イには15と14を比較してより大きい値である15が入ります。
∴ア=6,イ=9,ウ=12,エ=15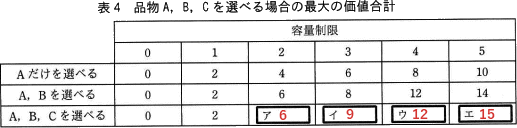
- 容量制限5であるエの価値合計を求めた際には、品物Cを選択した場合の価値合計がA,Bだけの組合せよりも大きくなりました。このため最後に選択されたのは品物Cになります。品物Cの容積は3ですから、続いて5から3を減じた容量制限2の列に注目します。容量制限2では、Aだけを選べる場合より、A,Bを選べる場合の価値合計が大きくなっています。したがって品物Bが選択されたことになります。つまり容量制限5で最大価値を実現する組合せは、品物Bが1つ、品物Cが1つです。
∴A=0,B=1,C=1
設問2
図1中のオ~クに入れる適切な字句を答えよ。
解答入力欄
- オ:
- カ:
- キ:
- ク:
解答例・解答の要点
- オ:t-size[s]
- カ:maxvalue[t]
- キ:choice[k]
- ク:maxvalue[V]
解説
〔オについて〕
動的計画法は以下のプロセスを繰り返して、容量制限ごとの最大価値を求めます。
∴オ=t-size[s]
〔カについて〕
カを含む命令文は上記の③の処理に相当します。tempには②で求めた価値合計が、maxvalue[t]には容量制限tにおける最大価値が格納されています。tempがmaxvalue[t]よりも大きければ、容量制限tにおける最大価値はtempになるので、maxvalue[t]をtempで更新することになります。つまりtempの代入先は maxvalue[t] です。
∴カ=maxvalue[t]
〔キについて〕
キを含むループは、容量制限から0まで遡りながら選んだ品物を出力する処理です。choice[t]には容量制限tのとき最後に選んだ品物が格納されており、ループの前に k ← V で初期化されているので、1回目のループではchoice[V]、すなわち最後に選んだ品物が出力されることになります。表4のケースであればchoice[5]が出力されます。
次に出力すべきは、容量制限から選んだ品物の容積を減じた数の小問題を解いたときに最後に選ばれた品物です。表4のケースであれば 5-3=2 なので、2回目のループではchoice[2]を出力しなければなりません。最後に選んだ品物の番号は直前に出力したchoice[k]に格納されているので、現在の容量制限を保持している変数kからchoice[k]の容積-size[choice[k]]を減じることになります。
∴キ=choice[k]
〔クについて〕
表4を見るとわかるように動的計画法の結果はmaxvalue[]の最終要素に格納されます。ナップザックの容量制限は変数Vが保持しているので、maxvalue[V]を指定すれば容量制限Vにおける価値合計を出力できます。
∴ク=maxvalue[V]
動的計画法は以下のプロセスを繰り返して、容量制限ごとの最大価値を求めます。
- 容量制限から、現在検証している品物(以下,品物X)の容積を減じる。
- ①で求めた数における小問題の結果に品物Xの価値を足す。
- ②で求めた合計価値と、これまでの最大価値を比較して大きい方をその容量制限における最大価値とする。
temp ← maxvalue[オ]+value[s]
の部分は上記の②に対応します。つまりオには対象となる小問題を指定するための式(①の部分)が入ります。容量制限がt、品物の容積がsize[s]なのでオは t-size[s] です。∴オ=t-size[s]
〔カについて〕
カを含む命令文は上記の③の処理に相当します。tempには②で求めた価値合計が、maxvalue[t]には容量制限tにおける最大価値が格納されています。tempがmaxvalue[t]よりも大きければ、容量制限tにおける最大価値はtempになるので、maxvalue[t]をtempで更新することになります。つまりtempの代入先は maxvalue[t] です。
∴カ=maxvalue[t]
〔キについて〕
キを含むループは、容量制限から0まで遡りながら選んだ品物を出力する処理です。choice[t]には容量制限tのとき最後に選んだ品物が格納されており、ループの前に k ← V で初期化されているので、1回目のループではchoice[V]、すなわち最後に選んだ品物が出力されることになります。表4のケースであればchoice[5]が出力されます。
次に出力すべきは、容量制限から選んだ品物の容積を減じた数の小問題を解いたときに最後に選ばれた品物です。表4のケースであれば 5-3=2 なので、2回目のループではchoice[2]を出力しなければなりません。最後に選んだ品物の番号は直前に出力したchoice[k]に格納されているので、現在の容量制限を保持している変数kからchoice[k]の容積-size[choice[k]]を減じることになります。
∴キ=choice[k]
〔クについて〕
表4を見るとわかるように動的計画法の結果はmaxvalue[]の最終要素に格納されます。ナップザックの容量制限は変数Vが保持しているので、maxvalue[V]を指定すれば容量制限Vにおける価値合計を出力できます。
∴ク=maxvalue[V]
設問3
本文中のケに入れる適切な字句を答えよ。
解答入力欄
- ケ:
解答例・解答の要点
- ケ:NV
解説
O(ビッグオー)記法では、計算量をO(n)やO(n2)ような形で表します。括弧の中に入る文字は、計算量を表す式から次数が最大の項以外を除き、さらにそこから係数を除いたものになります。
まずプログラムの各部分の計算量(ステップ数)は以下のようになっています。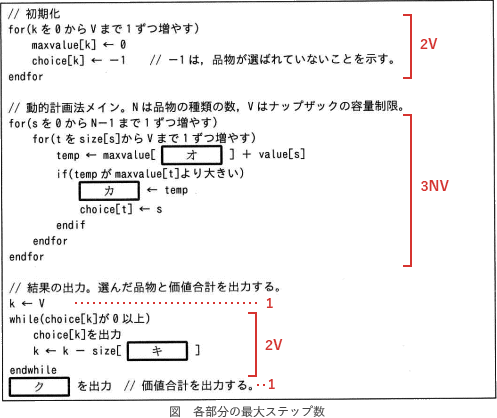 これを全て足すとプログラム全体の計算量を表す以下の式になります。
これを全て足すとプログラム全体の計算量を表す以下の式になります。
2V+3NV+1+2V+1
=3NV+4V+2
この式中で次数が最大の項は3NVなので、これ以外を式から除きます。さらに3NVの係数である3を除いたNVがケに入ります。
∴ケ=NV
以下は問題文の「ナップザック問題に対する動的計画法」をJavaScriptで実装したものです。細かな動作の確認等にお使いください。
まずプログラムの各部分の計算量(ステップ数)は以下のようになっています。

2V+3NV+1+2V+1
=3NV+4V+2
この式中で次数が最大の項は3NVなので、これ以外を式から除きます。さらに3NVの係数である3を除いたNVがケに入ります。
∴ケ=NV
以下は問題文の「ナップザック問題に対する動的計画法」をJavaScriptで実装したものです。細かな動作の確認等にお使いください。

