応用情報技術者過去問題 平成27年秋期 午後問3
⇄問題文と設問を画面2分割で開く⇱問題PDF問3 プログラミング
2分探索木に関する次の記述を読んで，設問1～4に答えよ。
2分探索木とは，全てのノードNに対して，次の条件が成立している2分木のことである。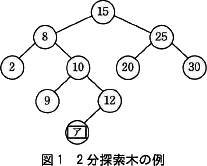
2分探索木を実現するために，ノードを表す構造体 Node を定義する。構造体 Node の構成要素を表1に示す。
構造体の実体を生成するためには，次のように書く。
new Node(key)
生成した構造体への参照が戻リ値となる。構造体の構成要素のうち，keyは引数keyの値で初期化され，leftとrightはnullで初期化される。
変数pが参照するノードをノードpという。ノードを参照する変数からそのノードの構成要素へのアクセスには"."を用いる。例えば，ノードpのキー値には，p.keyでアクセスできる。
なお，変数pの値がnullの場合，木は空である。
〔2分探索木でのノードの探索〕
与えられたキー値をもつノードを探索する場合，親から子の方向へ，木を順次たどりながら探索を行う。
探索する2分探索木にノードがない場合は，目的のノードが見つからず，探索は失敗と判断して終了する。探索する2分探索木にノードがある場合は，与えられたキー値と木の根のキー値を比較し，等しければ，目的のノードが見つかったので探索は成功と判断して終了する。与えられたキー値の方が小さければ左部分木に，大きければ右部分木に移動する。移動先の部分木でも同様に探索を続ける。
この手順によって探索を行う関数 search のプログラムを図2に示す。このプログラムでは，探索が成功した場合は見つかったノードへの参照を返し，失敗した場合はnullを返す。
〔2分探索木へのノードの挿入〕
2分探索木にノードを挿入する場合，探索と同様に，親から子の方向へ，木を順次たどりながら，適切な位置にノードを挿入する。
挿入する2分探索木にノードがない場合は，挿入するキー値のノードを作成する。挿入する2分探索木にノードがある場合は，挿入するキー値と木の根のキー値を比較し，挿入するキー値の方が小さければ左部分木に，大きければ右部分木に移動する。移動先の部分木でも同様の処理を続ける。
この手順によって挿入を行う関数 addNode のプログラムを図3に示す。このプログラムでは，挿入の結果として得られた2分探索木の根のノードへの参照を返す。ただし，このプログラムは，挿入するキー値と同じキー値をもつノードが2分探索木に既に存在するときは何もしない。
〔2分探索木からのノードの削除〕
2分探索木から，あるキー値をもつノードを削除する場合，次の(1)～(3)の手順を行う。
図4中の関数 extractMaxNode は，引数で指定されたノードを根とする2分探索木の中で最大のキー値をもつノードを木から削除し，削除されたノードへの参照を大域変数 extractedNode に設定した上で，削除した後の2分探索木の根のノードへの参照を返す。関数 extractMaxNode のプログラムを図5に示す。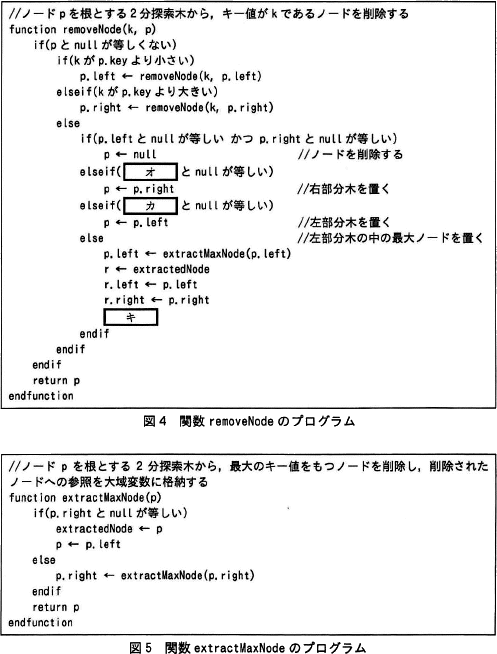
〔2分探索木の計算量〕
2分探索木における計算量は，木の高さに依存する。図2の関数 search を使ってn個のノードから成る2分探索木を探索する場合，想定される最大の計算量は，O(ク)である。木構造が完全2分木であれば，その計算量は最大でもO(ケ)で ある。
2分探索木とは，全てのノードNに対して，次の条件が成立している2分木のことである。
- Nの左部分木にある全てのノードのキー値は，Nのキー値よりも小さい。
- Nの右部分木にある全てのノードのキー値は，Nのキー値よりも大きい。
new Node(key)
生成した構造体への参照が戻リ値となる。構造体の構成要素のうち，keyは引数keyの値で初期化され，leftとrightはnullで初期化される。
変数pが参照するノードをノードpという。ノードを参照する変数からそのノードの構成要素へのアクセスには"."を用いる。例えば，ノードpのキー値には，p.keyでアクセスできる。
なお，変数pの値がnullの場合，木は空である。
〔2分探索木でのノードの探索〕
与えられたキー値をもつノードを探索する場合，親から子の方向へ，木を順次たどりながら探索を行う。
探索する2分探索木にノードがない場合は，目的のノードが見つからず，探索は失敗と判断して終了する。探索する2分探索木にノードがある場合は，与えられたキー値と木の根のキー値を比較し，等しければ，目的のノードが見つかったので探索は成功と判断して終了する。与えられたキー値の方が小さければ左部分木に，大きければ右部分木に移動する。移動先の部分木でも同様に探索を続ける。
この手順によって探索を行う関数 search のプログラムを図2に示す。このプログラムでは，探索が成功した場合は見つかったノードへの参照を返し，失敗した場合はnullを返す。
2分探索木にノードを挿入する場合，探索と同様に，親から子の方向へ，木を順次たどりながら，適切な位置にノードを挿入する。
挿入する2分探索木にノードがない場合は，挿入するキー値のノードを作成する。挿入する2分探索木にノードがある場合は，挿入するキー値と木の根のキー値を比較し，挿入するキー値の方が小さければ左部分木に，大きければ右部分木に移動する。移動先の部分木でも同様の処理を続ける。
この手順によって挿入を行う関数 addNode のプログラムを図3に示す。このプログラムでは，挿入の結果として得られた2分探索木の根のノードへの参照を返す。ただし，このプログラムは，挿入するキー値と同じキー値をもつノードが2分探索木に既に存在するときは何もしない。
2分探索木から，あるキー値をもつノードを削除する場合，次の(1)～(3)の手順を行う。
- 2分探索木にノードがない場合は，何もしないで処理を終了する。
- 削除するキー値と木の根のキー値を比較し，削除するキー値の方が小さければ左部分木に，大きければ右部分木に移動する。移動先の部分木でも同様の処理を続ける。
- 削除するキー値と木の根のキー値が等しい場合，削除するキー値をもつノードを削除するため，次の(3-1)～(3-3)を実行する。
- (3-1)
- 削除するノードが子ノードをもたない場合，そのノードを削除する。
- (3-2)
- 削除するノードが子ノードを一つだけもつ場合，削除するノードの位置にその子ノードを置く。
- (3-3)
- 削除するノードが左右両方に子ノードをもつ場合，削除するノードの左部分木の中で最大のキー値をもつノードを左部分木から取り除き，削除するノードの位置に置く。
図4中の関数 extractMaxNode は，引数で指定されたノードを根とする2分探索木の中で最大のキー値をもつノードを木から削除し，削除されたノードへの参照を大域変数 extractedNode に設定した上で，削除した後の2分探索木の根のノードへの参照を返す。関数 extractMaxNode のプログラムを図5に示す。
2分探索木における計算量は，木の高さに依存する。図2の関数 search を使ってn個のノードから成る2分探索木を探索する場合，想定される最大の計算量は，O(ク)である。木構造が完全2分木であれば，その計算量は最大でもO(ケ)で ある。
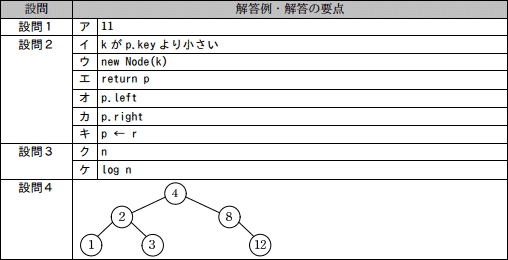
設問1
図1中のアに入れる適切な数を答えよ。
解答入力欄
- ア：
解答例・解答の要点
- ア：11
解説
〔アについて〕
図1「2分探索木の例」の[ア]に当てはまる数を考えます。
まず、問題文の5行目に「ここで，ノードのキー値は自然数で重複しないものとする」とあるため、[ア]には他のノードのキー値と重複しない自然数が入ることがわかります。そして、問題文の3行目と4行目より、2分探索木とは以下の条件が成立している2分木であることがわかります。
∴ア＝11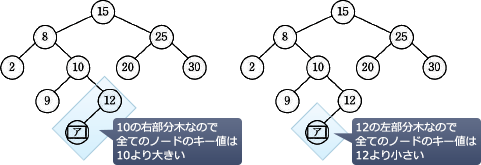
図1「2分探索木の例」の[ア]に当てはまる数を考えます。
まず、問題文の5行目に「ここで，ノードのキー値は自然数で重複しないものとする」とあるため、[ア]には他のノードのキー値と重複しない自然数が入ることがわかります。そして、問題文の3行目と4行目より、2分探索木とは以下の条件が成立している2分木であることがわかります。
- Nの左部分木にある全てのノードのキー値は、Nのキー値よりも小さい。
- Nの右部分木にある全てのノードのキー値は、Nのキー値よりも大きい。
∴ア＝11
設問2
図2～4中のイ～キに入れる適切な字句を答えよ。
解答入力欄
- イ：
- ウ：
- エ：
- オ：
- カ：
- キ：
解答例・解答の要点
- イ：k が p.key より小さい
- ウ：new Node(k)
- エ：return p
- オ：p.left
- カ：p.right
- キ：p ← r
解説
〔イについて〕
図2「関数 search のプログラム」の[イ]に当てはまる字句を考えます。
[イ]の条件式の結果が真のとき、以下の処理が実行されます。
∴イ＝k が p.key より小さい
〔ウについて〕
図3「関数 addNode のプログラム」の[ウ]に当てはまる字句を考えます。[ウ]は、図3の3行目の条件式の「pとnullが等しい」ときに行うべき処理です。
本文中に「変数pの値がnullの場合，木は空である」と記載があるように、「pとnullが等しい」ときとは挿入先の2分探索木にノードが存在しない場合を表します。〔2分探索木へのノードの挿入〕を読むと、「挿入する2分探索木にノードがない場合は，挿入するキー値のノードを作成する」とあるので、[ウ]には「挿入するキー値のノードを作成する」処理が入ると判断できます。
ノード作成のための命令は、表1の次行に「構造体の実体を生成するためには、次のように書く。new Node(key)」と説明されています。挿入するノードのキー値は、変数 k が保持しているため、k を引数にして「new Node(k)」を実行すれば良いことになります。よって、[ウ]には「new Node(k)」が入ります。
∴ウ＝new Node(k)
〔エについて〕
図3「関数 addNode のプログラム」の「エ」に当てはまる字句を考えます。
問題文の〔2分探索木へのノードの挿入〕には、「このプログラムでは，挿入の結果として得られた2分探索木の根のノードへの参照を返す」とあります。図3のソースには関数の戻り値を指定する文が存在しませんから、[エ]には挿入の結果として得られた2分探索木の根のノードへの参照を返す処理が入ります。
関数 addNode は、挿入するキー値(k)と、根ノードの参照(p)を引数としていますので、戻り値として p を返せば良いことになります。よって、[エ]には「return p」が入ります。
∴エ＝return p
〔オ、カについて〕
図4「関数 removeNode のプログラム」の[オ]に当てはまる字句を考えます。
〔2分探索木からのノードの削除〕の(3)に説明されている処理が、図4のプログラムの8行目から21行目の処理に対応しています。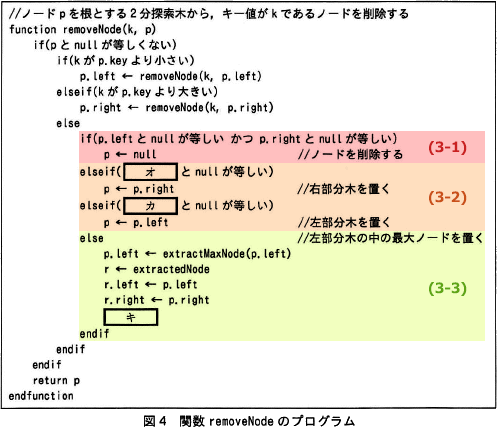
(3-2)の処理は、削除するノードが子ノードを（左右どちらか）1つだけ持つ場合に行われる処理です。このとき、存在する子ノードが左側であれば、削除するノードの位置に左部分木を移動し、存在する子ノードが右側であれば、削除するノードの位置に右部分木を移動します。
[オ]がnullのときに実行される「p←p.right」は、削除する位置に右側の部分木を移動させる処理ですから、条件式は「削除するノードの左の子ノードがない場合（＝削除するノードが右の子ノードを持つ場合）」であることがわかります。よって、[オ]には「p.left」が入ります。
同様の考え方で、「p←p.left」を実行する条件式は「p.rightがnullと等しい」となります。よって、[カ]には「p.right」が入ります。
∴オ＝p.left
カ＝p.right
〔キについて〕
図4「関数 removeNode のプログラム」の[キ]に当てはまる字句を考えます。
(3-3)の処理内容を確認します。
∴キ＝p ← r
図2「関数 search のプログラム」の[イ]に当てはまる字句を考えます。
[イ]の条件式の結果が真のとき、以下の処理が実行されます。
//8行目
return search(k, p.left) //左部分木を探索する
本文の〔2分探索木でのノードの探索〕の6行目に「与えられたキー値の方が小さければ左部分木に、大きければ右部分木に移動する」とあります。左部分木の探索に移るのは「木の根のキー値よりも与えられたキー値の方が小さい」場合です。木の根のキー値は「p.key」、探索しているキー値は「k」で参照できるため、[イ]には「kがp.keyより小さい」が入ります。return search(k, p.left) //左部分木を探索する
∴イ＝k が p.key より小さい
〔ウについて〕
図3「関数 addNode のプログラム」の[ウ]に当てはまる字句を考えます。[ウ]は、図3の3行目の条件式の「pとnullが等しい」ときに行うべき処理です。
本文中に「変数pの値がnullの場合，木は空である」と記載があるように、「pとnullが等しい」ときとは挿入先の2分探索木にノードが存在しない場合を表します。〔2分探索木へのノードの挿入〕を読むと、「挿入する2分探索木にノードがない場合は，挿入するキー値のノードを作成する」とあるので、[ウ]には「挿入するキー値のノードを作成する」処理が入ると判断できます。
ノード作成のための命令は、表1の次行に「構造体の実体を生成するためには、次のように書く。new Node(key)」と説明されています。挿入するノードのキー値は、変数 k が保持しているため、k を引数にして「new Node(k)」を実行すれば良いことになります。よって、[ウ]には「new Node(k)」が入ります。
∴ウ＝new Node(k)
〔エについて〕
図3「関数 addNode のプログラム」の「エ」に当てはまる字句を考えます。
問題文の〔2分探索木へのノードの挿入〕には、「このプログラムでは，挿入の結果として得られた2分探索木の根のノードへの参照を返す」とあります。図3のソースには関数の戻り値を指定する文が存在しませんから、[エ]には挿入の結果として得られた2分探索木の根のノードへの参照を返す処理が入ります。
関数 addNode は、挿入するキー値(k)と、根ノードの参照(p)を引数としていますので、戻り値として p を返せば良いことになります。よって、[エ]には「return p」が入ります。
∴エ＝return p
〔オ、カについて〕
図4「関数 removeNode のプログラム」の[オ]に当てはまる字句を考えます。
〔2分探索木からのノードの削除〕の(3)に説明されている処理が、図4のプログラムの8行目から21行目の処理に対応しています。
[オ]がnullのときに実行される「p←p.right」は、削除する位置に右側の部分木を移動させる処理ですから、条件式は「削除するノードの左の子ノードがない場合（＝削除するノードが右の子ノードを持つ場合）」であることがわかります。よって、[オ]には「p.left」が入ります。
同様の考え方で、「p←p.left」を実行する条件式は「p.rightがnullと等しい」となります。よって、[カ]には「p.right」が入ります。
∴オ＝p.left
カ＝p.right
〔キについて〕
図4「関数 removeNode のプログラム」の[キ]に当てはまる字句を考えます。
(3-3)の処理内容を確認します。
- 16行目
- p.leftを根とする2分探索木の中で最大のキー値を持つノードを削除し、削除した後の2分探索木の根のノードへの参照をp.leftに返します。さらに、削除したノードへの参照を extractedNode に代入します。
- 17行目
- rに削除したノードへの参照 extractedNode を代入します。
- 18行目
- rの左の子ノードにpの左の子ノードへの参照を設定します。
- 19行目
- rの右の子ノードにpの右の子ノードへの参照を設定します。
- 20行目
- キ
∴キ＝p ← r
設問3
本文中のク，ケに入れる適切な字句を答えよ。
解答入力欄
- ク：
- ケ：
解答例・解答の要点
- ク：n
- ケ：log n
解説
〔クについて〕
問題文の〔2分探索木の計算量〕には、「2分探索木における計算量は、木の高さに依存する」とあります。想定される最大の計算量を求めるには、比較回数が最大になる場合を考えます。
探索において比較回数が最大になるのは、全てのノードが一つの子ノードを持つ構造になっていて、探索するキー値が木の葉部分に位置している場合です。このときのノードの数をnとすると、木の高さはn-1です（木の高さは根から一番遠い葉までの枝の数です）。最大比較回数は「木の高さ＋1」で求めることができるため、「n-1+1＝n回」になります。以上より、計算量はO(n)となるので、[ク]には「n」が入ります。
∴ク＝n
〔ケについて〕
完全2分木とは、全てのノードが2つの子ノードを持ち、根から葉までの距離がどこでも等しい下図のような木構造です。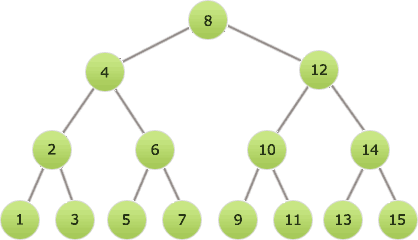
完全2分木の場合は、探索範囲を1／2ずつに狭めながら探索していきます。すなわち、n個のノードを1／2することをk回繰り返して、1つの値を見つけます。このことから、「n×1／2k＝1」の式を導くことができます。
n×1／2k＝1
n＝1／(1／2k)
n＝1×2k
n＝2k
より「k=log2n」となります。O記法では通常、底を省略して記述しますので、[ク]には「log n」が入ります。
※完全2分木を探索する計算量は、2分探索の計算量と同じです。
∴ク＝log n
問題文の〔2分探索木の計算量〕には、「2分探索木における計算量は、木の高さに依存する」とあります。想定される最大の計算量を求めるには、比較回数が最大になる場合を考えます。
探索において比較回数が最大になるのは、全てのノードが一つの子ノードを持つ構造になっていて、探索するキー値が木の葉部分に位置している場合です。このときのノードの数をnとすると、木の高さはn-1です（木の高さは根から一番遠い葉までの枝の数です）。最大比較回数は「木の高さ＋1」で求めることができるため、「n-1+1＝n回」になります。以上より、計算量はO(n)となるので、[ク]には「n」が入ります。
∴ク＝n
〔ケについて〕
完全2分木とは、全てのノードが2つの子ノードを持ち、根から葉までの距離がどこでも等しい下図のような木構造です。
n×1／2k＝1
n＝1／(1／2k)
n＝1×2k
n＝2k
より「k=log2n」となります。O記法では通常、底を省略して記述しますので、[ク]には「log n」が入ります。
※完全2分木を探索する計算量は、2分探索の計算量と同じです。
∴ク＝log n
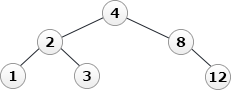
設問4
次の順でキー値の挿入と削除を行った後でノードqを根とする2分探索木を答えよ。2分探索木は，図1の例に倣って表現すること。
解答入力欄
- o：(図表で回答する問題のため解答入力欄はありません。)
解答例・解答の要点
- o：
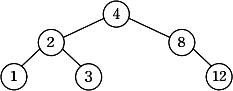
解説
- q ← null
- 2分探索木を空にするための処理です。
- q ← addNode(5, q)
- 手順2から手順9は図3の関数 addNode を使用してノードを追加していく処理です。関数 addNode は、pのノードのキー値と挿入するノードのキー値を比較しながら、2分探索木として適切な位置に子ノードを追加していきます。
最初は、木にノードがないので、根の位置にノードを生成します。
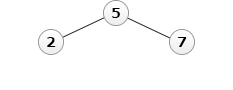
- q ← addNode(2, q)
- q ← addNode(7, q)
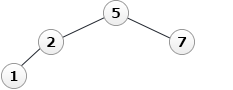
- q ← addNode(1, q)
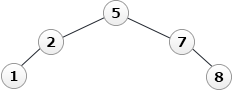
- q ← addNode(8, q)
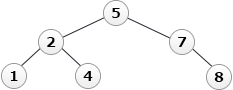
- q ← addNode(4, q)
- q ← addNode(3, q)
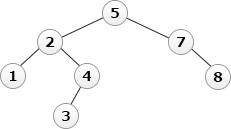
- q ← addNode(12, q)
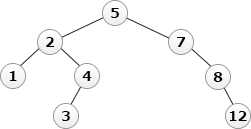
- q ← removeNode(5, q)
- キー値が5のノードを削除します。キー値が5のノードは2分探索木の根にあります。よって、removeNode関数の(3-3)の「削除するノードが左右両方に子ノードをもつ場合」に該当します。この場合は、「削除するノードの左部分木の中で最大のキー値をもつノードを左部分木から取り除き，削除するノードの位置に置く」という処理を行います。
左部分木の中で最大値は4ですから、- 4を取り除く
- 4の位置に3を置く
- 4の左の子ノードとして2を設定する
- 4の右の子ノードとして7を設定する
- 5の位置に4を置く
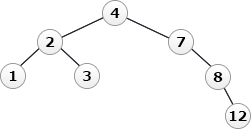
- q ← removeNode(7, q)
- キー値が7のノードを削除します。キー値が7のノードは右側の部分木のみをもっているため、(3-2)の「削除するノードが子ノードを一つだけもつ場合」に該当します。この場合は、「削除するノードの位置にその子ノードを置く」という処理を行います。つまり、7を取り除き、7の位置に8以降の部分木が収まります。
